Experiment on Fluids:
Finding the Velocity of a Fluid in a Confined Container
SUBJECT: Aeronautics
TOPIC: Fluid Velocity
DESCRIPTION: A set of mathematics problems dealing with fluid velocity.
CONTRIBUTED BY: Carol Hodanbosi
EDITED BY: Jonathan G. Fairman - August 1996
Purpose:
To calculate the velocity of a confined fluid, given the
cross-section area and velocity of another region.
Concept:
The drawing below is a cross-section of a circular cone attached
to a circular cylinder.
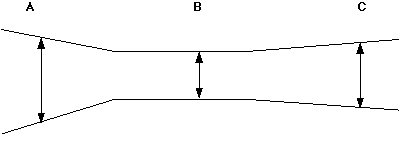
When a fluid (liquid or gas) is in a confined space, with no
change in pressure or temperature, one can use the equation of
continuity to find the velocity of the fluid if one knows the
cross-section area and velocity in one of the regions. The formula
for this is A1*V1 = A2*V2, where A is the cross-section area
of one location and V is the velocity for that location.
Analysis:
Given three different locations in a confined container, A, B, and
C, all having different radii, can you find the other two velocities
of the fluid, if the velocity at A is given?
- If the cross-section at A has a radius of 6 meters, can you
find the area of the slice through the cone
(Area = pi * r 2)?
(answer)
- If the velocity of the fluid at location A is 10.0 m/s,
and the radius at location B is 4.2 meters, can you find
the velocity at location B?
(answer)
- If the velocity at location C is 8.6 m/s, can
you find the radius at location C?
(answer)
Extension:
- If the radius of a fourth location, D, is one-half the
radius of A , how would the velocity at location D
compare to the velocity of the fluid at A? If D had
one-third the radius of A, compare the velocity of the
fluid at D to A. Explain your reasoning showing
calculations.
(answer)
Related Pages:
Aeronautics Activities
Aerospace Activities Page
Aerodynamics Index
Continuity Equation
Air Flow Rate
|
