To better understand the science of propulsion
it is necessary to use some mathematical ideas from
vector analysis.
Most people are introduced to vectors in high school or college,
but for the elementary and middle school students, or the mathematically-challenged:
DON'T PANIC!.
There are many complex parts to vector analysis and we aren't going there.
We are going to limit ourselves to the very basics.
Vectors allow us to look at complex, multi-dimensional problems
as a simpler group of one-dimensional problems.
We will be concerned mostly with definitions
The words are a bit strange, but the ideas are
very powerful as you will see.
Math and science were invented by humans to describe and
understand the world around us.
We live in a (at least) four-dimensional world governed by
the passing of time and three space dimensions; up and down,
left and right, and back and forth.
We observe that there are some quantities and processes in
our world that depend on the direction in which
they occur, and there are some quantities that do not depend
on direction. For example, the
volume
of an object, the three-dimensional space that an object occupies,
does not depend on direction.
If we have a 5 cubic foot block of iron and we move it up and down and
then left and right, we still have a 5 cubic foot block of iron.
On the other hand, the
location,
of an object does depend on direction.
If we move the 5 cubic foot block 5 miles to the
north, the resulting location is very different than
if we moved it 5 miles to the east.
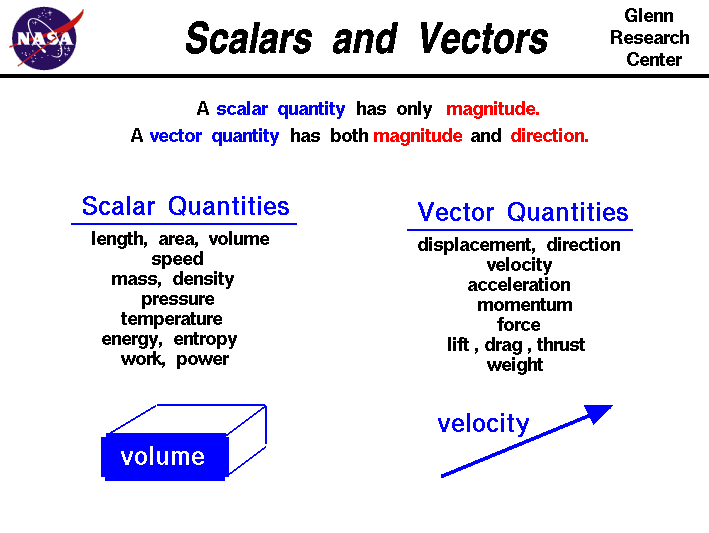
Mathematicians and scientists call a quantity
which depends on direction a vector quantity. A quantity
which does not depend on direction is called a scalar quantity.
Vector quantities have two characteristics, a magnitude and a direction.
Scalar quantities have only a magnitude. When
comparing
two vector quantities of the same type, you have to compare both
the magnitude and the direction. For scalars, you only have to
compare
the magnitude. When doing any mathematical operation on a vector quantity
(like adding, subtracting, multiplying ..) you have to
consider
both the magnitude and the direction. This makes dealing with vector
quantities a little more complicated than scalars.
On the slide we list some of the physical quantities discussed
in the
Beginner's Guide to Propulsion
and group them into either vector or scalar quantities. Of particular
interest, the
forces
which operate on a flying aircraft, the
weight,
thrust, and
aerodynmaic forces, are all
vector quantities. The resulting
motion
of the aircraft in terms of displacement, velocity, and
acceleration are also vector quantities.
These quantities can be determined by application of
Newton's laws
for vectors.
The scalar quantities include most of the
thermodynamic state
variables involved with the propulsion system, such as the
density,
pressure, and
temperature of the propellants.
The
energy,
work,
and
entropy
associated with the engines are also scalar quantities.
There are some quantities, like speed, which have
very special definitions for scientists. By definition,
speed is the scalar magnitude of a velocity vector. A car
going down the road has a speed of 50 mph. Its velocity
is 50 mph in the northeast direction. It can get very
confusing when the terms are used interchangeably!
While Newton's laws describe the resulting motion of a
solid, there are special equations which describe the motion
of fluids,
gases and liquids, through the propulsion system.
For any physical system, the
mass,
momentum, and
energy
of the system must be conserved. Mass and energy
are scalar quantities, while momentum is a vector
quantity. This results in a coupled set of equations,
called the
Navier-Stokes equations,
which describe how fluids behave when subjected to external forces.
These equations are the fluid equivalent of Newton's laws of motion
and are very difficult to solve and understand.
A simplified version of the equations called the
Euler equations
can be solved for some fluids problems.
Activities:
Guided Tours
Navigation ..

- Beginner's Guide Home Page
|
