As an object moves through the atmosphere, the gas molecules
of the atmosphere near the
rocket are disturbed and move around the object.
Aerodynamic
forces are generated between the gas and the object. The
magnitude of these forces depend on the shape of the object, the
speed of the object,
the mass
of the gas going by the object and on two other important properties
of the gas; the viscosity, or stickiness, of the gas and the
compressibility, or springiness, of the gas. To properly model
these effects, aerodynamicists use similarity parameters,
which are
ratios
of these effects to other forces present in the
problem. If two experiments have the same values for the similarity
parameters, then the relative importance of the forces are being
correctly modeled. Representative values for the properties of
air
are given on another page,
but the actual value of the parameter depends
on the
state of the gas
and on the
altitude.
Aerodynamic forces depend in a complex way on the viscosity of the
gas. As an object moves through a gas, the gas molecules stick to
the surface. This creates a layer of air near the surface, called a
boundary layer,
which, in effect, changes the shape of the
object. The flow of gas reacts to the edge of the boundary layer as if
it was the physical surface of the object. To make things more
confusing, the boundary layer may
separate
from the
body and create an effective shape much different from the physical
shape. And to make it even more confusing, the flow conditions in and
near the boundary layer are often unsteady (changing in time).
The boundary layer is very important in determining the
drag
of an object. To determine and predict these conditions,
aerodynamicists rely on
wind tunnel
testing and very sophisticated computer analysis.
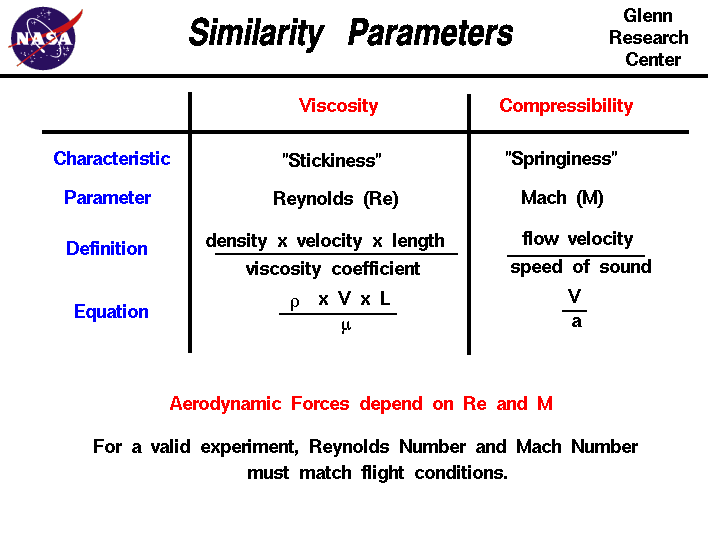
The important similarity parameter for viscosity is the
Reynolds number. The Reynolds number expresses the ratio of
inertial (resistant to change or motion) forces to viscous
(heavy and gluey) forces. From a detailed
analysis of the
momentum conservation equation,
the inertial forces are characterized by the product of the
density r times the velocity V times the
gradient of the velocity dV/dx. The viscous forces
are characterized by the viscosity coefficient mu times
the second gradient of the velocity d^2V/dx^2. The
Reynolds number Re then becomes:
Re = (r * V * dV/dx) / (mu * d^2V/dx^2)
Re = (r * V * L) / mu
where L is some characteristic length of the problem. If
the Reynolds number of the experiment and flight are close, then we
properly model the effects of the viscous forces relative to the
inertial forces. If they are very different, we do not correctly
model the physics of the real problem and predict incorrect levels of
the aerodynamic forces.
Aerodynamic forces also depend in a complex way on the
compressibility of the gas. As an object moves through the gas, the
gas molecules move around the object. If the object passes at a low
speed (typically less than 200 mph) the density of the fluid
remains constant. But for high speeds, some of the energy of the
object goes into compressing the fluid and changing the density,
which alters the amount of resulting force on the object. This
effect becomes more important as speed increases. Near and beyond the
speed of sound (about 330 m/s or 700 mph on earth),
shock waves are produced that affect
the lift and drag of the object. Again, aerodynamicists rely on wind
tunnel testing and sophisticated computer analysis to predict these
conditions.
The important similarity parameter for compressibility is the
Mach number - M, the ratio of the velocity
of the rocket to the speed of sound a.
M = V / a
So it is completely incorrect to measure a drag
coefficient at some low speed (say 200 mph) and apply that drag
coefficient at twice the speed of sound (approximately 1400 mph, Mach
= 2.0). The compressibility of the air alters the important
physics between these two cases.
The effects of compressibility and viscosity on lift are contained
in the lift coefficient and the effects on
drag are contained in the drag coefficient.
For propulsion systems, compressibility
affects the amount of mass that can pass
through an engine and the amount of thrust
generated by a rocket or turbine engine nozzle.
Activities:



Guided Tours
-
 Sources of Drag:
Sources of Drag:

-
 Speed of Sound:
Speed of Sound:

-
 Compressible Aerodynamics:
Compressible Aerodynamics:

Navigation ..

- Beginner's Guide Home Page
|
