|
|
Determining
Center of Gravity (Level 1) Activity
If so instructed by your teacher, print out a worksheet page for these
problems.
Open the slide called
Determining
Center of Gravity (with text) and read the explanation on how
an airplane in flight will rotate about a point in the airplane called
the center of gravity.
A Boeing 747-400 domestic
airplane is soaring the friendly skies (shown below). Use data from the
Boeing 747 Wikipedia
Website to complete Table 1. Estimate values for data you are unable
to locate in a reasonable amount of time. You willl have to select an engine to go on your
aircraft. You should be able to
find the length of the airplane (for the reference distances requested),
the mass of the engine, and the fuel capacity. The distances in Table
1 should be measured from a reference line that starts at the nose (front)
of the 747. Use the BACK key to return to this page.
Problem 1 will guide
you in the calculation to find the mass of the fuel.
All problems are expressed
in metric units.

| |
Mass (kg)
|
Distance from
Reference Line (m)
|
|
|
payload
|
|
|
d1
|
|
engine
|
|
|
d2
|
|
wings
|
|
|
d3
|
|
fuselage
|
|
|
d4
|
|
fuel
|
|
|
d5
|
|
vertical tail
|
|
|
d6
|
|
horizontal
tail
|
|
|
d7
|
Table 1 : Airplane
component masses and distances from reference line
-
- What is the fuel
capacity of the 747?
Fuel capacity
= Volume of fuel = ______________
- Assuming the density
of an average jet fuel is 0.75 g/ml, use the density equation,
density = mass
/ volume,
to calculate the
mass of the fuel. (Hint: You must convert from liters to milliliters.)
Mass of fuel =
______________
Record this value
for the mass of the fuel in Table 1.
- In Table 2, record
the weights of the components (parts) listed in Table 1.
(Hint:
Remember, F = mag = W. The acceleration due to gravity,
ag , is 9.8 m/s2.)
| |
Mass (kg)
|
Weight
(N)
|
|
|
payload
|
|
|
w1
|
|
engine
|
|
|
w2
|
|
wings
|
|
|
w3
|
|
fuselage
|
|
|
w4
|
|
fuel
|
|
|
w5
|
|
vertical
tail
|
|
|
w6
|
|
horizontal
tail
|
|
|
w7
|
Table
2 : Airplane component weights
- What does n equal?
[Hint:
The number n is the number of quantities being added together.]
n = _________
- What are the values
for i?
i = _________________________
- What is the total
weight W of the airplane?
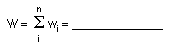
- What is the value
of the sum of the component weights times their distances from the reference
line (see the equation below)?
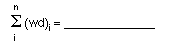
- Using your answers
from Problems 6 and 7, calculate the center of gravity.
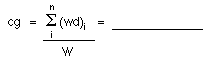
- After a long flight,
the amount of fuel left in the tanks is 20% of the initial amount. What
is the mass and weight of the fuel that is left? Record your answers
in Table 3.
| |
Mass (kg)
|
Weight
(N)
|
|
Remaining
Fuel
|
|
|
Table 3 : Remaining
Fuel Data
- Recalculate the
airplane's center of gravity with the reduced fuel weight.
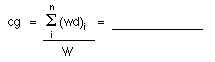
- Did the center
of gravity change?
- If
yes, by how many meters did the center of gravity move?
- If yes, did
the center of gravity move toward or away from the nose of the airplane?
- Do you think
the pilot would notice such a change in the center of gravity while
flying? Why?
|
