- Once released,
how much time will elapse before the supply package reaches the level
of the island?
(Hint:
Use the distance equation in the y-direction.)
Step 1: di
= 500 m; a = -9.8 m/s2 (gravity, negative sign indicates
downward direction); df = 0 m; vi = 0 m/s
where di = initial distance and df = final distance
Step 2: Solve
the equation df = ( 1 / 2 ) at2 + vit
+ di for t. So,
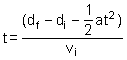
- Will the descent
time of the supply package change if the airplane's speed changes?
(a) Yes (b) No
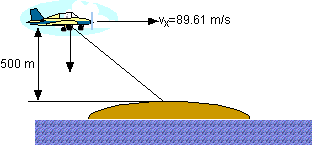
- At what (horizontal)
distance in front of the island should the package be released in order
to hit the island?
Step 1: During
descent the package moves forward a horizontal distance of dx.
v
= 89.61 m/s; t = 10.10 sec
Step
2: dx
= vt = 905.06 m. The airplane must release the package at least
905.06 m in front of the island.
- What is the package's
horizontal speed when it reaches the level of the island?
Neglecting
air resistance, it remains constant. vx = 89.61 m/s
- What is the package's
vertical speed when it reaches the level of the island?
Step 1: vi
= 0 m/s; a = -9.8 m/s2; t = 10.10 sec
Step
2: Solve
the equation a = (vf - vi )/t for vf.
So, vf = at + vi =
-98.98
m/s ( vf = vy )
- What will be the
package's flight angle with respect to the level of the island as it
descends?
Step 1: Draw
the diagram,
Step
2: vy
= -98.98 m/s; vx = 89.61 m/s
Step 3: tan
Q = vy / vx; Q
= tan-1(vy / vx) = 47.84
o
Suppose the
victims on the island can retrieve supply packages that land within
30 meters of the island. The length of the island is 50 meters along
the direction you are approaching.
- How far in front
of the island would the airplane have to release the supply package
for it to land 30 meters in front of the island?
dx(front)
= distance from problem #3 + 30 m =
935.06
m
- How far in front
of the island would the airplane have to release the supply package
for it to land 30 meters in back of the island?
dx(back)
= distance from problem #3 - 50 m - 30 m = 825.06 m
- Time1
will be the time on your watch when you release the package and it lands
30 meters in front of the island. Time2 will be the
time on your watch when you release the package and it lands 30 meters
in back of the island. Calculate the amount of time you have
to successfully drop the package, namely, time1- time2.
Step 1: time1
= 0 sec; vx = 89.61 m/s
Step
2: Solve
the equation dx = (vx )(time2) for
time2. Also realize that dx = dx(front)
- dx(back).
time2
= [ dx(front) - dx(back) ] / vx
= 1.23 sec. Therefore, time1 - time2 = 1.23
sec
- What could be done
to decrease the package's speed when it reaches the ground?
Use a parachute.
