|
|
-
Aircraft
Trajectory Activity
If so instructed by your teacher, print out a worksheet
page for these problems.
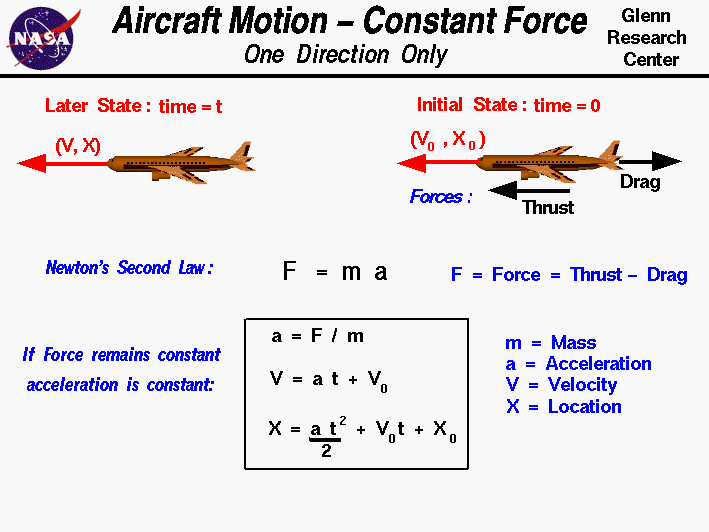
Open the slide called
Aircraft Motion (with text)
and read the explanation on how to calculate speed, distance, acceleration,
and time in simple aircraft motion with force and mass constant.
You are the copilot
on a Boeing 747. The Captain plans to make various changes in speed (velocity).
Assume that your aircraft
is in simple aircraft motion with force and mass constant. As the copilot
you must be able to correctly give the Captain the results of the changes
in velocity. Using the motion equations shown above, solve for the unknown
values to complete the following tables. Assume that X0 is
0.
Initial
Velocity
(V0) km./hr.
|
Acceleration
(a) km./hr.2
|
Time
(t) hr.
|
Final
Velocity
(V) km./hr.
|
|
300
|
50
|
2
|
|
|
|
50
|
3
|
500
|
|
250
|
|
5
|
450
|
|
400
|
25
|
|
600
|
|
600
|
|
10
|
400
|
TABLE 1
Initial
Velocity
(V0) km./hr.
|
Acceleration
(a) km/hr.2
|
Time
(t) hr.
|
Final
Velocity
(V) km./hr.
|
Distance
Traveled
(X) km.
|
|
350
|
100
|
2
|
|
|
|
|
20
|
3
|
260
|
|
|
280
|
|
2
|
|
640
|
|
250
|
30
|
|
370
|
|
|
500
|
|
5
|
|
2250
|
TABLE 2
|
