
|
This page is intended for college or high school students.
For younger students, a simpler explanation of the information on this page is
available on the
Kids Page.
|
Most modern passenger and military aircraft are powered by
gas turbine engines, which are also called
jet engines. Jet engines come in a variety
of shapes and sizes.
To evaluate the performance of a turbine engine, we have to determine
the
thrust
generated by the engine, the
fuel consumed
to produce the thrust, and the
weight
of the engine itself.
The weight of the engine is important because it contributes
to the overall
weight
of the
airplane.
Aircraft
range,
rate of climb,
and maneuvering capability depend on the
thrust to weight
ratio of the aircraft.
On this page we present a simple model for estimating the weight of a
gas turbine engine. The model is used in the
EngineSim
computer program. The modeling method is the same for each type of
gas turbine engine, although the number of components and the
values of some parameters are different for each type of engine.
On this page we use a
turbofan
engine as an example.
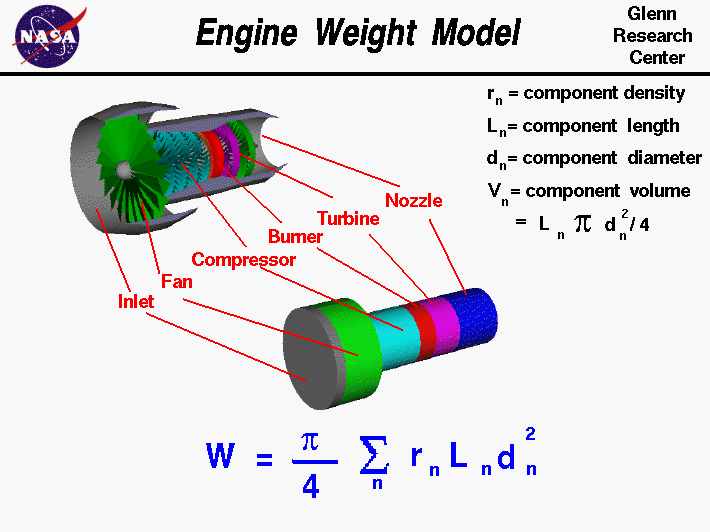
In general, the weight W of any object with a uniform
distribution of material of
density r
is equal to the density times the volume of the object:
W = r * V
For our model, we represent each major
component
of the engine by a cylinder. Each component has a distinct length L
and diameter d. The
volume
of a cylinder is:
V = pi * L * d^2 / 4
where pi is the ratio of the circumference to the diameter of a
circle and equal to 3.1415...
If we know the volume and the density of each major component, we can
calculate the weight wn of each component. The weight W of the
engine is the the sum of the weights of the components:
W = sum (wn)
On the figure we use the Greek letter "sigma" to denote the sum over
all the components.
For our model, we must determine a density rn for each component.
Using the
compressor
as an example, it is obvious that in the real component the material is
not evenly distributed. There are rows of blades separated by air spaces
and connected to a central shaft. The blades and the shaft are made of different
materials. The external cowling is made of a third material. For our model,
we are going to represent all of the different materials by just one
component average material. We determine the density of the
component average material by
calibrating our model using the weight and volume of
the component for an existing
engine. If we are using EngineSim, and decide to change the material of
the compressor from titanium blades to aluminum blades, we change the
compressor average material density by multiplying by the ratio of the density ofaluminum to the density of titanium, and then re-compute the weight.
Here is a table of the density of materials which are used in jet engines:
| Material |
T Lim K |
Density kg/m^3 |
| Aluminum |
500 |
2726 |
| Titanium |
833 |
4693 |
| Stainless Steel |
1111 |
7633 |
| Nickel Alloy |
1388 |
8252 |
| Nickel Crystal |
1666 |
8252 |
| Ceramic |
1666 |
2630 |
We have included the temperature limits on the table because weight is only
one consideration in picking the materials used in an engine. EngineSim checks
the computed
temperature
in each part of the
engine cycle
against the temperature limits of the component and signals the user if
a temperature limit is exceeded.
The model which is given here accounts for the change in weight for both
geometric changes (change in length or diameter of the component) and
for a change in material for the component.
Notice that the procedure outlined here is just a way to
estimate the weight of a new engine. It is just a model, but
it gives the engineer an indication of how the weight changes based
on design decisions. Engineers often use estimates and models when
making design decisions. The estimate has to be checked during testing.
In the case of aircraft engine weight, this value is closely monitored
during design refinement by actually measuring the weight of the components.
Activities:
Guided Tours
Navigation ..

- Beginner's Guide Home Page
|
