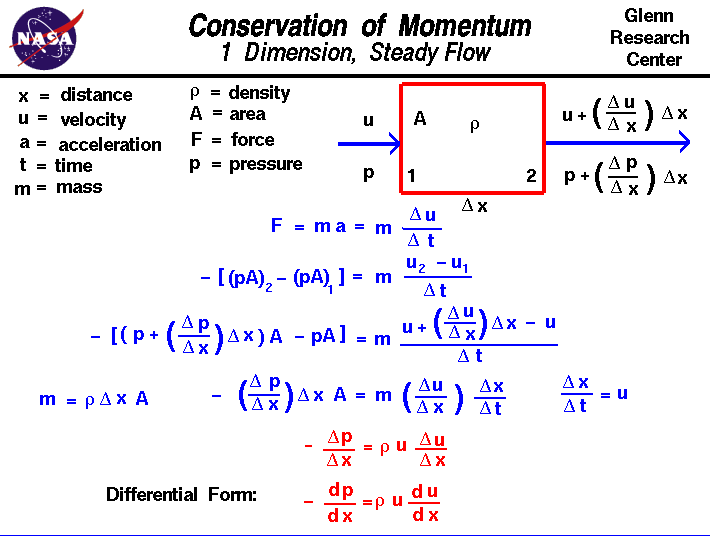
The conservation of momentum is a fundamental concept of physics
along with the
conservation of energy
and the
conservation of mass.
Momentum is defined to be the mass of an object multiplied by the velocity
of the object.
The conservation of momentum states that,
within some problem domain, the amount of momentum remains constant;
momentum is neither created nor destroyed, but only changed
through the action of forces as described by Newton's
laws of motion.
Dealing with momentum is more difficult than dealing with mass and energy because
momentum is a
vector quantity
having both a magnitude and a direction. Momentum is conserved in all three
physical directions at the same time. It is even more difficult when dealing with a
gas
because forces in one direction can affect the momentum in another direction
because of the collisions of many molecules.
On this slide, we will present a very, very simplified flow problem
where properties only change in one direction.
The problem is further simplified by considering a steady flow which does
not change with time and by limiting the forces to only those
associated with the
pressure.
Be aware that real flow problems are much
more complex
than this simple
example.
Let us consider the flow of a gas through a domain in which flow properties
only change in one direction, which we will call "x". The gas enters the domain
at station 1 with some velocity u and some pressure p
and exits at station 2 with a different value
of velocity and pressure. For simplicity, we will assume that
the density r remains constant within the domain
and that the area A through which the
gas flows also remains constant. The location of stations 1 and 2 are separated
by a distance called del x. (Delta is the little triangle on the slide
and is the Greek letter "d". Mathematicians often use this symbol to denote
a change or variation of a quantity. The web print font does not support
the Greek letters, so we will just call it "del".)
A change with distance is referred to as a gradient
to avoid confusion with a change with time which is called a rate.
The velocity gradient is indicated by del u / del x;
the change in velocity per
change in distance. So at station 2, the velocity is given by the velocity
at 1 plus the gradient times the distance.
u2 = u1 + (del u / del x) * del x
A similar expression gives the pressure
at the exit:
p2 = p1 + (del p / del x) * del x
Newton's
second law of motion states
that force F is equal to the change in momentum with
respect to time. For an object with constant mass
m this reduces to the mass times acceleration a.
An acceleration is a change in velocity with a change in time
(del u / del t). Then:
F = m * a = m * (del u / del t)
The force in this problem
comes from the pressure gradient. Since pressure is a force per unit area,
the net force on our fluid domain is the pressure times the area at the
exit minus the pressure times the area at the entrance.
F = - [(p * A)2 - (p * A)1] = m * [(u2 - u1) / del t]
The minus sign at
the beginning of this expression is used because gases move from a region
of high pressure to a region of low pressure; if the pressure increases with
x, the velocity will decrease. Substituting for our expressions for velocity
and pressure:
- [{(p + (del p / del x) * del x} * A) - (p * A)] = m * [(u + (del u / del x) * del x - u) /
del t]
Simplify:
- (del p / del x) * del x * A = m * (del u / del x) * del x / del t
Noting that (del x / del t) is the
velocity and that the mass is the density r times the volume (area times del x):
- (del p / del x) * del x * A = r * del x * A * (del u / del x) * u
Simplify:
- (del p / del x) = r * u * (del u / del x)
The del p / del x and del u / del x
represent the pressure and velocity gradients.
If we shrink our domain down to differential sizes, these gradients become differentials:
- dp/dx = r * u * du/dx
This is a one dimensional, steady form of
Euler's Equation.
It is interesting to note that the pressure drop
of a fluid (the term on the left) is proportional to both the value of the
velocity and the gradient of the velocity.
A solution of this momentum equation gives us the form of the
dynamic pressure
that appears in
Bernoulli's Equation.
Activities:
Guided Tours
Navigation ..


- Beginner's Guide Home Page
|
