 V&V Home
Archive
Tutorial
V&V Home
Archive
Tutorial
Examining Spatial (Grid) Convergence
Introduction
The examination of the spatial convergence of a simulation is a straight-forward method for determining the ordered discretization error in a CFD simulation. The method involves performing the simulation on two or more successively finer grids. The term grid convergence study is equivalent to the commonly used term grid refinement study.
As the grid is refined (grid cells become smaller and the number of cells in the flow domain increase) and the time step is refined (reduced) the spatial and temporal discretization errors, respectively, should asymptotically approaches zero, excluding computer round-off error.
Methods for examining the spatial and temporal convergence of CFD simulations are presented in the book by Roache. They are based on use of Richardson's extrapolation. A summary of the method is presented here.
A general discussion of errors in CFD computations is available for background.
We will mostly likely want to determine the error band for the engineering quantities obtained from the finest grid solution. However, if the CFD simulations are part of a design study that may require tens or hundreds of simulations, we may want to use one of the coarser grids. Thus we may also want to be able to determine the error on the coarser grid.
Grid Considerations for a Grid Convergence Study
The easiest approach for generating the series of grids is to generate a grid with what one would consider fine grid spacing, perhaps reaching the upper limit of one's tolerance for generating a grid or waiting for the computation on that grid to converge. Then coarser grids can be obtained by removing every other grid line in each coordinate direction. This can be continued to create additional levels of coarser grids. In generating the fine grid, one can build in the n levels of coarser grids by making sure that the number of grid points in each coordinate direction satisfies the relation
N = 2n m + 1
where m is an integer. For example, if two levels of coarser grids are desired (i.e. fine, medium, and coarse grids) then the number of grid points in each coordinate direction must equal 4 m + 1. The m may be different for each coordinate direction.
The WIND code has a grid sequencing control that will solve the solution on the coarser grid without having to change the grid input file, boundary condition settings, or the input data file. Further, the converged solution on the coarser grid then can be used directly as the initial solution on the finer grid. This option was originally used to speed up convergence of solutions; however, can be used effectively for a grid convergence study.
It is not necessary to halve the number of grid points in each coordinate direction to obtain the coarser grid. Non-integer grid refinement or coarsening can be used. This may be desired since halfing a grid may put the solution out of the asymptotic range. Non-integer grid refinement or coarsening will require the generation of a new grid. It is important to maintain the same grid generation parameters as the original grid. One approach is to select several grid spacings as reference grid spacings. One should be the grid spacing normal to the walls. Others may be spacings at flow boundaries, at junctures in the geometry, or at zonal interfaces. Upon picking the ratio as which the grid is to be refined or coarsened, this same ratio is applied to these spacings. The number of grid points are then adjusted according to grid quality parameters, such as grid spacing ratio limits. The surface and volume grids are then generated using the same methods as the original grid. The grid refinement ratio should be a minimum of r >= 1.1 to allow the discretization error to be differentiated from other error sources (iterative convergence errors, computer round-off, etc...).
Order of Grid Convergence
The order of grid convergence involves the behavior of the solution error defined as the difference between the discrete solution and the exact solution,
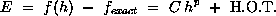
where C is a constant, h is some measure of grid spacing, and p is the order of convergence. A "second-order" solution would have p = 2.
A CFD code uses a numerical algorithm that will provide a theoretical order of convergence; however, the boundary conditions, numerical models, and grid will reduce this order so that the observed order of convergence will likely be lower.
Neglecting higher-order terms and taking the logarithm of both sides of the above equation results in:
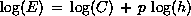
The order of convergence p can be obtained from the slope of the curve of log(E) versus log(h). If such data points are available, the slope can be read from the graph or the slope can be computed from a least-squares fit of the data. The least-squares will likely be inaccurate if there are only a few data points.
A more direct evaluation of p can be obtained from three solutions using a constant grid refinement ratio r,
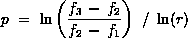
The order of accuracy is determined by the order of the leading term of the truncation error and is represented with respect to the scale of the discretization, h. The local order of accuracy is the order for the stencil representing the discretization of the equation at one location in the grid. The global order of accuracy considers the propagation and accumulation of errors outside the stencil. This propagation causes the global order of accuracy to be, in general, one degree less than the local order of accuracy. The order of accuracy of the boundary conditions can be one order of accuracy lower than the interior order of accuracy without degrading the overall global accuracy.
Asymptotic Range of Convergence
Assessing the accuracy of code and caluculations requires that the grid is sufficiently refined such that the solution is in the asymptotic range of convergence. The asymptotic range of convergence is obtained when the grid spacing is such that the various grid spacings h and errors E result in the constancy of C,
C = E / hp
Another check of the asymptotic range will be discussed in the section on the grid convergence index.
Richardson Extrapolation
Richardson extrapolation is a method for obtaining a higher-order estimate of the continuum value (value at zero grid spacing) from a series of lower-order discrete values.
A simulation will yield a quantity f that can be expressed in a general form by the series expansion:
f = fh=0 + g1 h + g2 h2 + g3 h3 + ...
where h is the grid spacing and the functions g1, g2, and g3 are independent of the grid spacing. The quantity f is considered "second-order" if g1 = 0.0. The fh=0 is the continuum value at zero grid spacing.
If one assumes a second-order solution and has computed f on two grids of spacing h1 and h2 with h1 being the finer (smaller) spacing, then one can write two equations for the above expansion, neglect third-order and higher terms, and solve for fh=0 to estimate the continuum value,
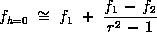
where the grid refinement ratio is:
r = h2 / h1
The Richardson extrapolation can be generalized for a p-th order methods and r-value of grid ratio (which does not have to be an integer) as:
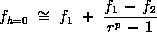
Traditionally, Richardson extrapolation has been used with grid refinement ratios of r = 2. Thus, the above equation simplifies to:
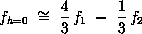
In theory, the above equations for the Richardson extrapolation will provide a fourth-order estimate of fh=0, if f1 and f2 were computed using exactly second-order methods. Otherwise, it will be a third-order estimate. In general, we will consider fh=0 to be p+1 order accurate. Richardson extrapolation can be applied for the solution at each grid point, or to solution functionals, such as pressure recovery or drag. This assumes that the solution is globally second-order in addition to locally second-order and that the solution functionals were computed using consistent second-order methods. Other cautions with using Richardson extrapolation (non-conservative, amplification of round-off error, etc...) are discussed in the book by Roache.
For our purposes we will assume f is a solution functional (i.e. pressure recovery). The fh=0 is then as an estimate of f in the limit as the grid spacing goes to zero. One use of fh=0 is to report the value as the an improved estimate of f1 from the CFD study; however, one has to understand the caveats mentioned above that go along with that value.
The other use of fh=0 is to obtain an estimate of the discretization error that bands f obtained from the CFD. This use will now be examined.
The difference between f1 and fh=0 is one error estimator; however, this requires consideration of the caveats attached to fh=0.
We will focus on using f1 and f2 to obtain an error estimate. Examining the generalized Richardson extrapolation equation above, the second term on the right-hand side can be considered to be an an error estimator of f1. The equation can be expressed as:
A1 = E1 + O( hp+1, E12)
where A1 is the actual fractional error defined as:
A1 = ( f1 - fh=0 ) / fh=0
and E1 is the estimated fractional error for f1 defined as:
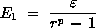
where the relative error is defined as:
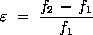
This quantity should not be used as an error estimator since it does not take into account r or p. This may lead to an underestimation or overestimation of the error. One could make this quantity artificially small by simply using a grid refinement ratio r close to 1.0.
The estimated fractional error E1 is an ordered error estimator and a good approximation of the discretization error on the fine grid if f1 and f2 were obtained with good accuracy (i.e. E1<1). The value of E1 may be meaningless if f1 and fh=0 are zero or very small relative to f2-f1. If such is the case, then another normalizing value should be used in place of f1.
If a large number of CFD computations are to be performed (i.e for a DOE study), one may wish to use the coarser grid with h2. We will then want to estimate the error on the coarser grid. The Richardson extrapolation can be expressed as:
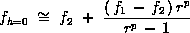
The estimated fractional error for f2 is defined as:
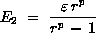
Richardson extrapolation is based on a Taylor series representation as indicated in Eqn. \ref{eq:series}. If there are shocks and other discontinuities present, the Richardson extrapolation is invalid in the region of the discontinuity. It is still felt that it applies to solution functionals computed from the entire flow field.
Grid Convergence Index (GCI)
Roache suggests a grid convergence index GCI to provide a consistent manner in reporting the results of grid convergence studies and perhaps provide an error band on the grid convergence of the solution. The GCI can be computed using two levels of grid; however, three levels are recommended in order to accurately estimate the order of convergence and to check that the solutions are within the asymptotic range of convergence.
A consistent numerical analysis will provide a result which approaches the actual result as the grid resolution approaches zero. Thus, the discretized equations will approach the solution of the actual equations. One significant issue in numerical computations is what level of grid resolution is appropriate. This is a function of the flow conditions, type of analysis, geometry, and other variables. One is often left to start with a grid resolution and then conduct a series of grid refinements to assess the effect of grid resolution. This is known as a grid refinement study.
One must recognize the distinction between a numerical result which approaches an asymptotic numerical value and one which approaches the true solution. It is hoped that as the grid is refined and resolution improves that the computed solution will not change much and approach an asymptotic value (i.e. the true numerical solution). There still may be error between this asymptotic value and the true physical solution to the equations.
Roache has provided a methodology for the uniform reporting of grid refinement studies. "The basic idea is to approximately relate the results from any grid refinement test to the expected results from a grid doubling using a second-order method. The GCI is based upon a grid refinement error estimator derived from the theory of generalized Richardson Extrapolation. It is recommended for use whether or not Richardson Extrapolation is actually used to improve the accuracy, and in some cases even if the conditions for the theory do not strictly hold." The object is to provide a measure of uncertainty of the grid convergence.
The GCI is a measure of the percentage the computed value is away from the value of the asymptotic numerical value. It indicates an error band on how far the solution is from the asymptotic value. It indicates how much the solution would change with a further refinement of the grid. A small value of GCI indicates that the computation is within the asymptotic range.
The GCI on the fine grid is defined as:
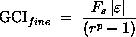
where Fs is a factor of safety. The refinement may be spatial or in time. The factor of safety is recommended to be Fs=3.0 for comparisons of two grids and Fs=1.25 for comparisons over three or more grids. The higher factor of safety is recommended for reporting purposes and is quite conservative of the actual errors.
When a design or analysis activity will involve many CFD simulations (i.e. DOE study), one may want to use the coarser grid h2. It is then necessary to quantify the error for the coarser grid. The GCI for the coarser grid is defined as:
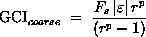
It is important that each grid level yield solutions that are in the asymptotic range of convergence for the computed solution. This can be checked by observing two GCI values as computed over three grids,
GCI23 = rp GCI12
Required Grid Resolution
If a desired accuracy level is known and results from the grid resolution study are available, one can then estimate the grid resolution required to obtain the desired level of accuracy,
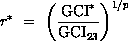
Independent Coordinate Refinement and Mixed Order Methods
The grid refinement ratio assumes that the refinement ratio r applies equally in all coordinate directions (i,j,k) for steady-state solutions and also time t for time-dependent solutions. If this is not the case, then the grid convergence indices can be computed for each direction independently and then added to give the overall grid convergence index,
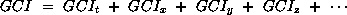
Effective Grid Refinement Ratio
If one generates a finer or coarser grid and is unsure of the value of grid refinement ratio to use, one can compute an effective grid refinement ratio as:
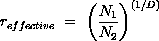
where N is the total number of grid points used for the grid and D is the dimension of the flow domain. This effective grid refinement ratio can also be used for unstructured grids.
Example Grid Convergence Study
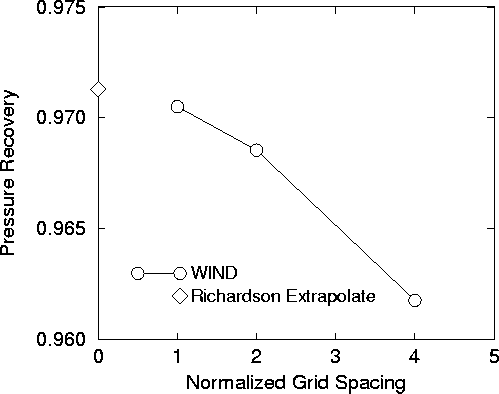
The following example demonstrates the application of the above procedures in conducting a grid convergence study. The objective of the CFD analysis was to determine the pressure recovery for an inlet. The flow field is computed on three grids, each with twice the number of grid points in the i and j coordinate directions as the previous grid. The number of grid points in the k direction remains the same. Since the flow is axisymmetric in the k direction, we consider the finer grid to be double the next coarser grid. The table below indicates the grid information and the resulting pressure recovery computed from the solutions. Each solution was properly converged with respect to iterations. The column indicated by "spacing" is the spacing normalized by the spacing of the finest grid.
| Grid | Normalized Grid Spacing | Pressure Recovery, Pr |
|---|---|---|
| 1 | 1 | 0.97050 |
| 2 | 2 | 0.96854 |
| 3 | 4 | 0.96178 |
The figure below shows the plot of pressure recoveries with varying grid spacings. As the grid spacing reduces, the pressure recoveries approach an asymptotic zero-grid spacing value.
We determine the order of convergence observed from these results,
p = ln[ ( 0.96178 - 0.96854 ) / ( 0.96854 - 0.97050 ) ] / ln(2) = 1.786170
The theoretical order of convergence is p=2.0. The difference is most likely due to grid stretching, grid quality, non-linearities in the solution, presence of shocks, turbulence modeling, and perhaps other factors.
We now can apply Richardson extrapolation using the two finest grids to obtain an estimate of the value of the pressure recovery at zero grid spacing,
Prh=0 = 0.97050 +
( 0.97050 - 0.96854 ) / ( 21.786170 - 1 )
= 0.97050 + 0.00080 = 0.97130
This value is also plotted on the figure below.
The grid convergence index for the fine grid solution can now be computed. A factor of safety of FS=1.25 is used since three grids were used to estimage p. The GCI for grids 1 and 2 is:
GCI12 = 1.25 | ( 0.97050 - 0.96854 ) / 0.97050 | / ( 21.786170 - 1 ) 100% = 0.103083%
The GCI for grids 2 and 3 is:
GCI23 = 1.25 | ( 0.96854 - 0.96178 ) / 0.96854 | / ( 21.786170 - 1 ) 100% = 0.356249%
We can now check that the solutions were in the asymptotic range of convergence,
0.356249 / ( 21.786170 0.103083 ) = 1.002019
which is approximately one and indicates that the solutions are well within the asymptotic range of convergence.
Based on this study we could say that the pressure recovery for the supersonic ramp is estimated to be Pr = 0.97130 with an error band of 0.103% or 0.001.
VERIFY: A Fortran program to Perform Calculations Associated with a Grid Convergence Study
The Fortran 90 program verify.f90 was written to carry out the calculations associated with a grid convergence study involving 3 or more grids. The program is compiled on a unix system through the commands:
f90 verify.f90 -o verify
It reads in an ASCII file (prD.do) through the standard input unit (5) that contains a list of pairs of grid size and value of the observed quantity f.
verify < prD.do > prD.out
It assumes the values from the finest grid are listed first. The output is then written to the standard output unit (6) prD.out. The output from the of {\tt verify} for the results of Appendix A are:
--- VERIFY: Performs verification calculations ---
Number of data sets read = 3
Grid Size Quantity
1.000000 0.970500
2.000000 0.968540
4.000000 0.961780
Order of convergence using first three finest grid
and assuming constant grid refinement (Eqn. 5.10.6.1)
Order of Convergence, p = 1.78618479
Richardson Extrapolation: Use above order of convergence
and first and second finest grids (Eqn. 5.4.1)
Estimate to zero grid value, f_exact = 0.971300304
Grid Convergence Index on fine grids. Uses p from above.
Factor of Safety = 1.25
Grid Refinement
Step Ratio, r GCI(%)
1 2 2.000000 0.103080
2 3 2.000000 0.356244
Checking for asymptotic range using Eqn. 5.10.5.2.
A ratio of 1.0 indicates asymptotic range.
Grid Range Ratio
12 23 0.997980
--- End of VERIFY ---
Examples of Grid Converence Studies in the Archive
A grid convergence study is performed in the Supersonic Wedge case.Examples of Grid Converence Studies in Literature
Other examples of grid convergence studies that use the procedures outlined above can be found in the book by Roache and the paper by Steffen et al..
NPARC Alliance Policy with Respect to Grid Converence Studies
For the WIND verification and validation effort, it is suggested that the above procedures be used when conducting and reporting results from a grid convergence study.
Last Updated: Wednesday, 10-Feb-2021 09:38:58 EST