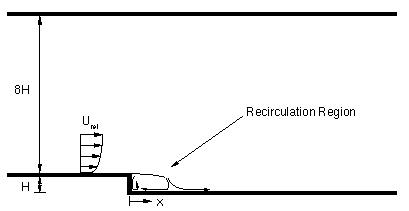
Figure 1: Schematic of Backward-Facing Step.

Figure 1: Schematic of Backward-Facing Step.
This study focuses on the incompressible flow over a backward-facing step, measured experimentally by Driver & Seegmiller. This geometry has a step height to tunnel exit height ratio of 1:9 which helps to minimize the freestream pressure gradient due to sudden expansion. The experimental configuration also had a step height to tunnel width ratio of 1:12 to minimize three-dimensional effects. Data from the original experimentors is listed in the file bstepdata.txt. All calculations presented below are for the case of zero degree divergence of the top wall and were computed using a two-dimensional grid.
All of the archive files of this validation case are available in the Unix compressed tar file bstep.tar.Z. The files can then be accessed by the commands
uncompress bstep.tar.Z
tar -xvof bstep.tar
A 238 x 185 single-zone mesh was generated to model the region from x/H = -105 to +50. The grid was clustered to the solid surfaces such that y+ = 1. Downstream of the step, 55 points were used in the recirculation region with ten of them placed within y+ = 30. The grid was also clustered in the streamwise direction near the recirculation region to improve resolution.
This grid is provided below in Plot3d (two-dimensional, multiple-grid, unformatted, whole) and common file format. The coordinates in both files are in units of feet and the step height H is 0.5 inches.
| Plot3D | Common Grid |
| bstep.x | bstep.cgd |
The initial (freestream) conditions were generated by WIND at startup. The Chien k-epsilon model was initialized from the existing solution and turbulent viscosity of the SST model after 35000 iterations.
For the NPARC cacluations, the Baldwin-Lomax model is used for the first 1000 iterations. At that time, the Chien k-epsilon model is initialized from the existing turbulent viscosity.
Since this flow was modeled using a single zone, the step itself was modeled using a viscous wall fringe boundary around a hole. Downstream of the step, the J1 boundary was also set to viscous wall. On the Jmax boundary, the first 12 grid points were treated as an inviscid wall in order to try and match the boundary layer profile at x/H=-4. The remainder of this boundary was modeled using the viscous wall condition. The I1 boundary from J=55 to 185 was set to an arbitrary inflow, and the Imax plane was set to a confined outflow. For more information about implementing these boundary conditions on the grid, have a look at the GMAN journal file.
The computation is performed using the time-marching capabilities of WIND to march to a steady-state (time asymptotic) solution. Local time stepping is used at each iteration. The time-marching is performed until the convergence criteria is achieved. For these cases, the solution was monitored for changes in integral flow properties such as mass flow rate, displacement thickness, and momentum thickness.
The input data file for WIND is bstep.dat.
The WIND flow solver is run, creating the following output files:
|
Chien k-epsilon |
Menter SST |
|||||
| Num. of Iterations |
solution file |
output file |
variable Cµ |
Num. of Iterations |
solution file |
output file |
|
90000 |
off |
100000 |
||||
Note that the Chien k-epsilon solutions were initialized from the corresponding Menter SST solutions at 35000 iterations. Thus, the k-epsilon model was run 55000 iterations after initialization. In examining the convergence of the Chien k-epsilon solutions, it appears that the model was nearly converged at 75000 iterations. The additional iterations were performed to confirm this.
Also note that the SST solution was initially run with an outflow mass flow rate of 3.25 lbm/sec to match that specified for the NPARC code. However, the NPARC code only provided a mass flow rate of 3.20 lbm/sec. At 75000 iterations with the SST model, the WIND boundary condition was modified to match this actual value. After 25000 additional iterations, the mass flow rate was nearly settled out on the correct value. However, the L2 residual had not completely settled.
The WIND k-epsilon solutions were initialized from the SST solution at 35000 iterations. At this time, the outflow mass flow rate was adjusted to the correct value.
The point to be emphasized is that a significant portion of these iterations were spent settling out the flowfield to obtain the proper mass flow rate. If these cases were to be run again, the user could expect somewhat better convergence (perhaps as much as 20000 iterations savings).
Convergence information can be obtained from the WIND output files listed above by using the resplt utility program.
Since this study compares both NPARC and WIND results, a common post processor (bsteppost.f) was used. This program reads the solution from an NPARC restart file, which means that the WIND solutions must be converted prior to running it.
The figure below shows the velocity profiles at several axial locations. All of the profiles are normalized by the flow velocity just before the backstep (Uref = 44.2 m/s). Upstream of the step, all of the solutions are virtually identical. Within the recirculation region, however, there are noticeable differences. The NPARC and WIND k-epsilon solutions are nearly indistinguishible and appear to provide the best match to the experimental data.
Use of the variable Cµ option in the WIND k-epsilon model causes the flow to reattach further downstream, but does not predict the rest of the velocity profile as well as the standard k-epsilon model.
The WIND SST model predicts the flow to reattach the furthest downstream.
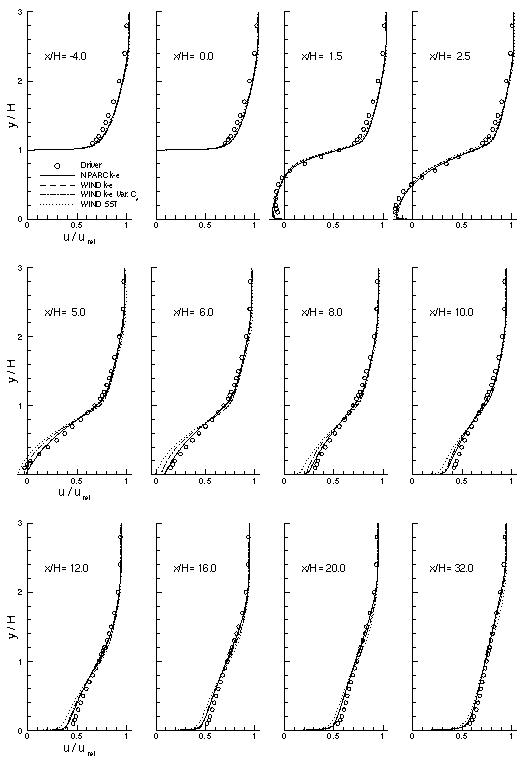
Figure 2: Velocity Profiles at Several Axial Locations.
These findings relative to the extent of the recirculation region are reiterated in the following figure, which shows the predicted skin friction coefficient. Both the NPARC and WIND k-epsilon models predict the reattachment to occur too far upstream and display under and overshoots relative to the data.
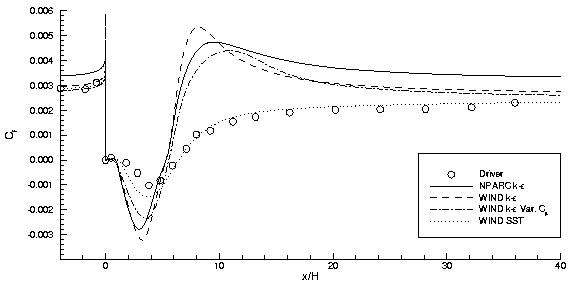
Figure 3: Skin Friction Coefficient Downstream of Backstep.
According to Avva, Smith and Singhal this overshoot can be reduced by increasing the number of points below y+ = 30. For a mesh with ten points inside this region, the present results agree with those presented by Avva.
The variable Cµ option tends to reduce the turbulent viscosity within the separation region, thus making the flow appear more laminar-like and reducing the magnitude of the skin friction. The predicted reattachment location is also shown to move downstream.
Unlike for the velocity profiles, the WIND SST model seems to provide relatively good agreement with the skin friction data. The table below lists the reattachment location predicted by each model.
| Model | xr/H |
| NPARC k-e WIND k-e WIND k-e Var. Cµ WIND SST Experiment |
5.31 5.30 5.55 6.43 6.26 |
The next figure shows the turbulent kinetic energy profiles at several axial locations. Upstream of the backstep, the flow is similar to that of a flat plate and one can see that the peak value in turbulent kinetic energy is underpredicted by the SST model due to the form of the k-omega model used in the near-wall region. This difference appears to propagate downstream as the SST model consisently predicts a lower peak value than the k-epsilon model at each axial station.
As with the velocity profiles shown above, there is close agreement between the NPARC and WIND k-epsilon solutions. One can also notice the reduction in turbulent kinetic energy, especially within the recirculation region, caused by the use of the variable Cµ option. This occurs because the variable Cµ option effectively increases the turbulent dissipation rate within the recirculation zone.
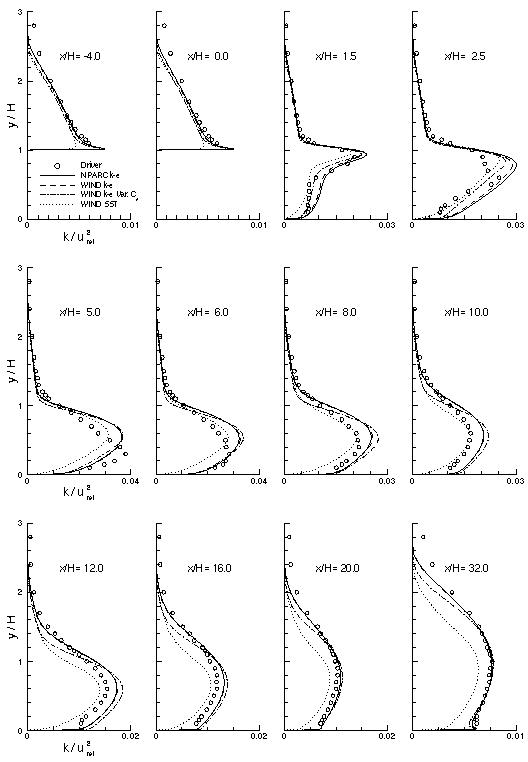
Figure 4: Turbulent Kinetic Energy Profiles.
The corresponding Reynolds stress profiles are shown below. Here again there is excellent agreement between the NPARC and WIND k-epsilon solutions, except near x/H=0 where the WIND solution predicts a more rapid increase in the downward component of velocity.
Far downstream the k-epsilon model overpredicts the Reynolds stress which corresponds with the overprediction in skin friction presented above. One can also observe how the variable Cµ correction noticeably reduces the peak turbulent viscosity (and consequently the Reynolds stress) within the recirculation region.
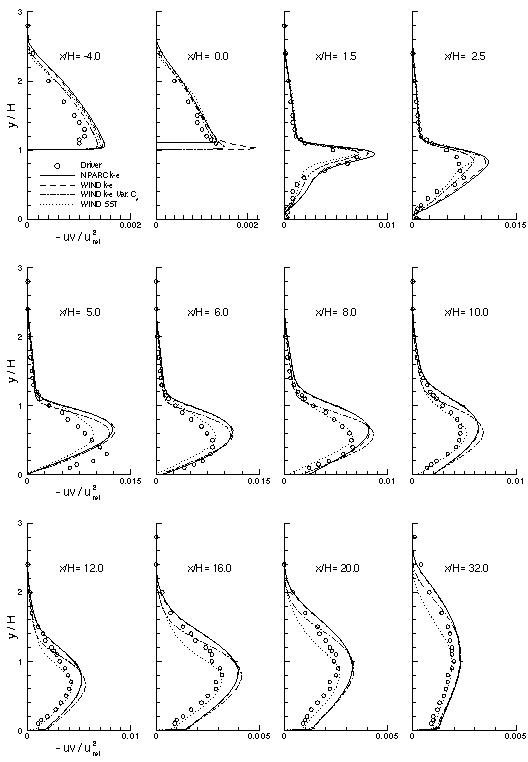
Figure 5: Reynolds Stress Profiles.
Avva, R.K., Smith, C.E., and Singhal, A.K., "Comparative Study of High and Low Reynolds Number Versions of k-epsilon Models," AIAA Paper 90-0246, Jan. 1990.
Driver, D.M. and Seegmiller, H.L., "Features of a Reattaching Turbulent Shear Layer in Divergent Channel Flow," AIAA Journal, Vol. 23, No. 2, Feb. 1985, pp. 163-171.
Yoder, Dennis A., and Georgiadis, Nicholas J., "Implementation and Validation of the Chien k-epsilon Turbulence Model in the WIND Navier-Stokes Code," AIAA Paper 99-0745, Jan. 1999.
This case was created on December 11, 1998 by Dennis A. Yoder, who may be contacted at
NASA Lewis Research Center, MS 86-7
21000 Brookpark Road
Cleveland, Ohio 44111
Phone: (216) 433-8716
e-mail: Dennis.A.Yoder@lerc.nasa.gov