One of the most exciting plays in the game of soccer is a free kick.
Players are often able to curve the flight of the ball into the net
by imparting a spin to the ball. Soccer players call this effect "bending"
and it is caused by
aerodynamic forces on the ball.
All that is necessary to create lift is
to turn a flow of air. The airfoil of a wing turns a flow, but so
does a spinning ball. The
details of how the force is generated are fairly complex, but the
magnitude of the force F depends on the radius of the ball b,
the spin of the ball s, the velocity V
of the kick, the density r of the air, and an
experimentally determined lift coefficient Cl.
F = Cl * 4 /3 * (4 * pi^2 * r * s * V * b^3)
where pi is the number 3.14159 .. the ratio of the circumference to
the diameter of a circle.
As the force acts on the ball, it is deflected along its
flight path. If we neglect the viscous forces on the ball, which
slow it down and change the magnitude and direction of the force, we
have a constant force always acting perpendicular (at a right
angle) to the flow direction. The resulting
flight path
is a circular arc.
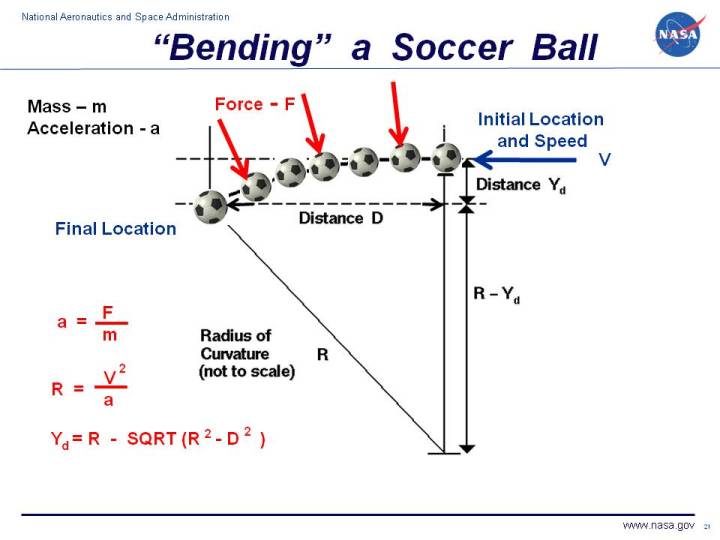
On the figure, we see the trajectory of the soccer ball as it moves
from right to left. The radius of curvature R of the flight path
depends on the velocity V of the kick and the acceleration a
produced by the side force.
R = V^2 / a
We can determine this acceleration from
Newton's second law of motion using the force for a spinning ball
and the mass m of the ball.
a = F / m
Since the radius of curvature
depends on the force, all the factors that affect the force will also
affect the trajectory.
Collecting all the information into one equation:
R = (3 * m * V) / (16 * Cl * r * s * b^3 * pi^2)
We can use this equation to make some predictions about the
trajectory of a spinning ball.
Higher spin s produces a smaller radius of curvature R and
a sharper curve.
Higher velocity V produces a larger radius of curvarture and
a straighter curve.
A ball with a smaller mass, like a ping-pong ball, has a lower radius
of curvature and curves more.
At higher altitudes,
the density r is lower producing a larger radius of curvature and a
straighter path.
The altitude effect helps to explain some of the complaints at the recent
World Cup, 2010. The games were played at 10 different stadiums, some at sea
level and some high in the mountains. It is much harder to bend a
kick at high altitude.
Knowing the radius of curvature and the distance of the kick D
we can also calculate the distance that the ball is deflected (Yd) along the flight path.
There is a right triangle formed by the radius of curvature R,
the distance D at the top, and the radius
of curvature minus the deflection distance R - Yd on the
right. We can then use the
Pythagorean Theorem
to relate the sides of this triangle:
R^2 = D^2 + (R - Yd)^2
Now let's do a little algebra:
R^2 - D^2 = (R -Yd)^2
sqrt(R^2 - D^2) = R -Yd
Yd = R - sqrt(R^2 - D^2)
You can investigate the effect of
aerodynamics on kicking a soccer ball by using the
SoccerNASA Java Applet.
Have fun !
You can
use the browser "Back" button to return to this page. If you
want your own copy of SoccerNASA to
play with, you can download it
for free.
Activities:
Guided Tours
Navigation ..

- NASA Soccer Home Page
- Beginner's Guide Home Page
|
