Most modern passenger and military aircraft are powered by
gas turbine engines, also called jet
engines. All types of jet engines have
some parts in common.
All jet engines have a compressor to
increase the pressure of the incoming air. There are currently two
principal compressor designs found on jet engines: the axial
compressor, in which the air flows parallel to the axis of
rotation, and the centrifugal compressor,
in which the air is turned perpendicular to the axis of rotation. In
either design, the job of the compressor is to increase the pressure
of the flow. We measure the increase by the compressor pressure
ratio (CPR), which is the ratio of the air total pressure pt exiting
the
compressor to the air pressure entering the compressor. This number
is always greater than 1.0.
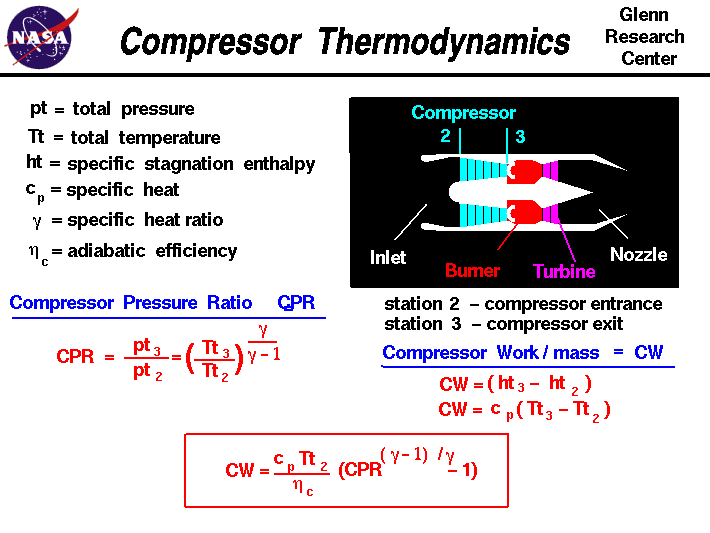
Referring to our station
numbering, the compressor entrance is station 2 and the compressor exit
is station 3.
The CPR is equal to pt3 divided by pt2, as shown on the
slide.
CPR = pt3 / pt2 >= 1.0
To produce the increase in pressure, the compressor must perform
work on the flow. In the axial
compressor, cascades of small airfoils are mounted on a shaft that
turns at a high rate of speed. Several rows, or stages, are
usually used to produce a high CPR, with each stage producing a small
pressure increase. In the centrifugal compressor, an additional
pressure increase results from turning the flow radially,
radiating from or converging to a common center.
Since no external heat is being added to or extracted from
the compressor during
the pressure increase, the process is
isentropic. The total temperature
ratio Tt3 / Tt2 across the compressor is related to the pressure ratio by the
isentropic flow equations.
Tt3 / Tt2 = (pt3 / pt2) ^((gam -1) / gam)
where gam is the ratio of
specific heats.
Work must be done to turn the shaft on which the compressor is
mounted. From the conservation of energy, the
compressor work per mass of airflow CW is equal to the change in
the specific enthalpy ht of the flow from
the entrance to the exit of the compressor.
CW = ht3 - ht2
The term
"specific" means per mass of airflow. The enthalpy at the
entrance and exit is related to the total temperature Tt at those
stations.
CW = cp * (Tt3 - Tt2)
Performing
a little algebra, we arrive at the equation:
CW = [cp * Tt]2 * [CPR ^((gam -1) / gam) - 1] / nc
that relates the work required to turn the compressor to the
compressor pressure ratio, the incoming total temperature, some
properties of the gas, and an
efficiency factor nc. The efficiency factor is included to
account for the actual performance of the compressor as opposed to
the ideal, isentropic performance. In an ideal world, the value of
the efficiency would be 1.0; in reality, it is always less than 1.0.
So additional work is needed to overcome the inefficiency of the
compressor to produce a desired CPR. The work is provided by the
power turbine, which is connected
to the compressor by the central shaft.
Notice that the CPR is related to the total temperature ratio
across the compressor. Since the CPR is always greater than 1.0 and
the value of gam, the ratio of specific heats, is about 1.4
for air, the total temperature ratio is also greater than 1.0.
Air heats up as it passes through the compressor.
There are
temperature limits
on the materials of the compressor.
On some engines, the temperature at the exit of the compressor becomes a
design constraint, a factor limiting the engine performance.
You can now use
EngineSim
to study the effects
of different materials on engine operation.
Activities:
Guided Tours
-
 EngineSim - Engine Simulator:
EngineSim - Engine Simulator:

-
 Compressor:
Compressor:

Navigation ..

- Beginner's Guide Home Page
|
