Math and science were invented by humans to describe and
understand the world around us.
We observe that there are some quantities and processes in
our world that depend on the direction in which
they occur, and there are some quantities that do not depend
on direction.
Mathematicians and scientists call a quantity
which depends on direction a vector quantity. A quantity
which does not depend on direction is called a scalar quantity.
A
vector quantity
has two characteristics, a magnitude and a direction. When
comparing
two vector quantities of the same type, you have to compare both
the magnitude and the direction.
On this slide we describe the method for adding two vectors.
Vector addition is one aspect of a larger vector algebra which we are
not going to present at this web site. Vector addition is presented
here because it occurs quite often in the study of rockets
and because it demonstrates some fundamental differences between
vectors and scalars.
Vectors are usually denoted on figures by an arrow.
The length of the arrow indicates the magnitude and the
tip of the arrow indicates the direction. The vector is
labeled with an alphabetical
letter with a line over the top to distinguish it from a scalar.
We will denote the magnitude of the vector by the symbol |a|. The direction
will be measured by an angle phi relative to a coordinate
axis x. The coordinate axis y is perpendicular to
x.
Note: The coordinate axes x and y are themselves
vectors! They have a magnitude and a direction. You first
encounter coordinates axes when you learn to graph. So, you have
been using vectors for some time without even knowing it!
If we construct a dashed line from the tip of the vector a
running parallel to the x-axis, it cuts the y-axis at a location we
label ay. Similarly, a line from the tip of the vector
parallel to the y-axis cuts the x-axis at ax.
The quanities ax and ay are called the
components
of the vector and both are scalar quantites.
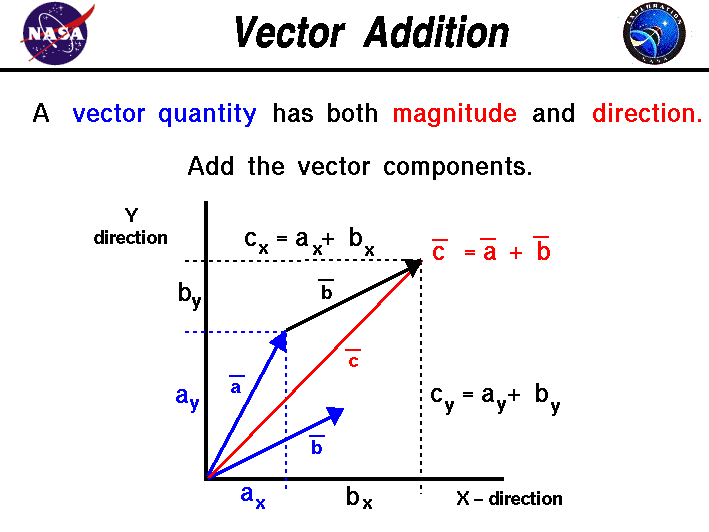
To add two vectors, a and b,
we first break each vector into its components, ax and ay,
and bx and by,
as shown on the figure. From the rules which govern the
equality
of vectors, the blue vector b is equal to the black vector b
because it has equal equal length and equal direction.
Now since the components of vector a and
vector b are scalars, we can add the x-components to generate
the x-component of new vector c:
cx = ax + bx
Similarly, we can add the y-components:
cy = ay + by
The new components, cx and cy, completely define the
new vector c by specifying both the magnitude and the direction.
Looking carefully at the diagram, we see that adding two vectors produces
a new vector which is not in the direction of either of the
original vectors, and whose magnitude is not equal to the sum
of the magnitudes of the original vectors.
Vector algebra is very different from scalar algebra because it must
account for both magnitude and direction.
Note: On this slide, for simplicity, we have developed the
components in only two dimensions; there are two coordinate axes.
In reality, there are three spatial dimensions and three components of
all forces. This is important in our derivation of the
general equations of
with motion
for flight trajectories and for the
Navier-Stokes and
Euler equations which
describe the forces and resulting motion of fluids in the engine.
We can break very complex, three-dimensional, vector problems into
only three scalar equations.
Guided Tours
-
 Vectors:
Vectors:

-
 Rocket Translation:
Rocket Translation:

Activities:
Related Sites:
Rocket Index
Rocket Home
Beginner's Guide Home
|
