Getting a Little "Lift" out of Calculus Part I: Answers

  1. When I printed out the enlarged picture of the plotter view panel, I found the curve to cover 6.5 cm. Because of this, I divided it into 12 rectangles with width .5 cm each (see Figure 1). I then took the height measurements of each rectangle and recorded them in a spreadsheet (see Table 1).
  2. The program displays the plot from 0 to 1 square foot, so I converted the X-axis to (0 to 144) square inches. I then divided the displayed 144 inches by the measured 6.5 cm to find an X-scaling factor of 22.15. On the Y-axis, 1.0 psi was equivalent to 6.0 cm, which gives the Y-scaling factor of .1666. On the spread sheet, I have multiplied by the approtiate scaling factors.
  3. I then multiplied the scaled values to find the total area under the curve. This gave a value of 68.4 lbs which represented the lift force.
  4. I found the following functions to represent the curves (shown in Figure 2):

    f1(x) = 14.81

    f2(x) = .0065 x + 13.87

  5. I finished by solving the following integral:

    Integral (X=0 to X=144) [f1(x) - f2(x)] dx

    135.3 - 66.3 = 69.0 lbs
  6. The value calculated by FoilSim is 66 lbs, so both answers compare favorably.
 

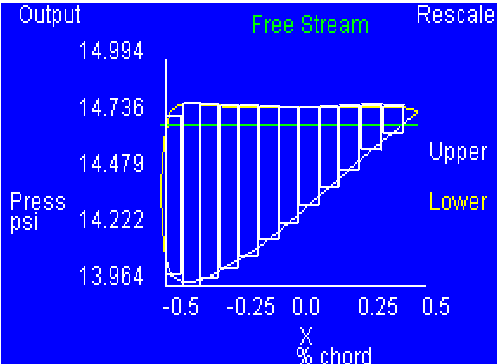Figure 1

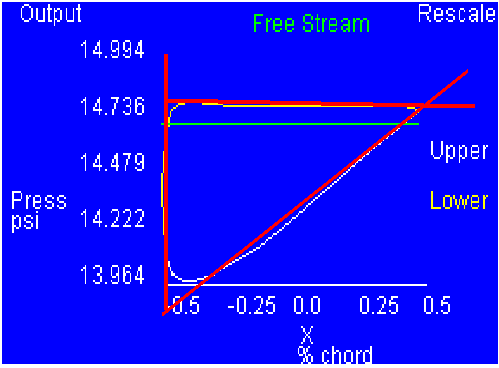Figure 2

Table 1

Measured

Scaled

Rectangle

Width (cm)

Height (cm)

Width (sq. in.)

Height (lbs/sq. in.)

Area (lbs)

1

0.50

4.2

11.07

.7

7.7

2

0.50

5.0

11.07

.83

9.2

3

0.50

4.6

11.07

.766

8.5

4

0.50

4.4

11.07

.733

8.1

5

0.50

4.1

11.07

.683

7.5

6

0.50

3.6

11.07

.6

6.6

7

0.50

3.1

11.07

.516

5.7

8

0.50

2.6

11.07

.433

4.8

9

0.50

2.1

11.07

.35

3.9

10

0.50

1.7

11.07

.283

3.1

11

0.50

1.1

11.07

.183

2.0

12

0.50

.7

11.07

.117

1.3

Total (in lbs)

68.4


Please send any comments to:
Curator: Tom.Benson@grc.nasa.gov
Responsible Official: Kathy.Zona@grc.nasa.gov