
|

|
+ Text Only Site
+ Non-Flash Version
+ Contact Glenn
|
|
|

|
Density Activity
Answers
|

|
|
Altitude (meters)
|
Density (kg/m3)
|
|
0
|
1.22859
|
|
100
|
1.21686
|
|
200
|
1.20521
|
|
400
|
1.18217
|
|
800
|
1.13711
|
|
1600
|
1.05093
|
|
3200
|
0.89362
|
|
6400
|
0.63345
|
|
12800
|
0.27386
|
- Use the data that you recorded to produce a line graph. Use
altitude as the independent variable and make a line of best fit.
See graph.
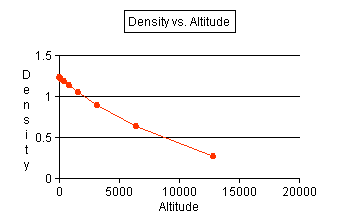
- Use your graph to make a general statement on the relationship
of density to altitude. As altitude
increases, the density decreases with a decreasing rate.
- Why do you think this happens?
The atoms and molecules in air are
held close to the earth by gravity since it has a greater effect
close to the surface. The farther away from the surface, the fewer
particles there are; so the density is lower.
- Convert the following altitudes from meters to feet.
a) 1000 meters = 3281
feet
b) 2500 meters = 8202
feet
c) 6500 meters = 21325 feet
- After converting your altitudes to feet, you can calculate (or
predict) the temperature at these altitudes by using the following
equation: T = 59 - .00356 (h), where h = altitude (in feet). Your
temperatures will be in degrees F. Calculate the temperature for
each of the altitudes in Question 4.
a) T1 =
59 - .00356(3281) = 47.3*F
b)
T2 = 59 - .00356(8202) =
29.8*F
c)
T3 = 59 - .00356(21325) =
-16.9*F
- Use AtmosModeler to check your answers. Be sure the "Units" menu next
says "Imperial" to compute in
English units. Input each of the altitudes (in feet).
Compare your answers for temperature to the AtmosModeler temperatures
and explain how any differences may have occurred.
a) T1 =
47o F
b)
T2 = 29o F
c)
T3 = -17o F
T1 and T3 appear to be rounded correctly. But T2 is rounded
down instead of up.
- The temperature may now be used to calculate the pressure of
the air at each altitude. Using the equation p = 2116 (T + 459.7 /
518.6)5.256 where T = degrees F and p =
lbs/in2, find the pressure that corresponds to each of
your temperatures.
a)
T1 = 13.04 lb/sq in (89.86
K - Pascals)
b)
T2 = 10.84 lb/sq in (74.7 K -
Pascals)
c)
T3 =6.4 lb/sq in (44.08 K -
Pascals)
- How does the pressure change compared to a change in
altitude?
The pressure goes down as the altitude
increases.
- Use a model or table to compare the change in altitude,
density, temperature, and pressure at the same time. Include an
explanation.
|
Altitude (feet)
|
Density (slugs/ft3)
|
Temperature (oF)
|
Pressure (lbs/sq in)
|
|
3281
|
.00216
|
47
|
13.04
|
|
8202
|
.00186
|
29
|
10.84
|
|
21,325
|
.00121
|
-17
|
6.4
|
|
Increase
|
Decrease
|
Decrease
|
Decrease
|
As the altitude increases, the
density of the air decreases. This, in turn, causes the pressure
to drop, as does the temperature.
|
Related Pages:
Standards
Activity
Worksheet
Lesson Index
Aerodynamics Index
|
|
|
|
