We live in a world that is defined by three spatial dimensions and one
time dimension. Objects move within this domain in two ways.
An object translates,
or changes location, from one
point to another.
And an object
rotates,
or changes its orientation.
In general, the motion of an object
involves both translation in all
three directions,
and rotation about
three principle axes.
On this page we will consider only the translation of an object.
We can specify the location of the object at
any time t by specifying three coordinates x, y,
and z on an orthogonal coordinate system. An
orthogonal coordinate system
has each
of its coordinate directions perpendicular to all other coordinate directions.
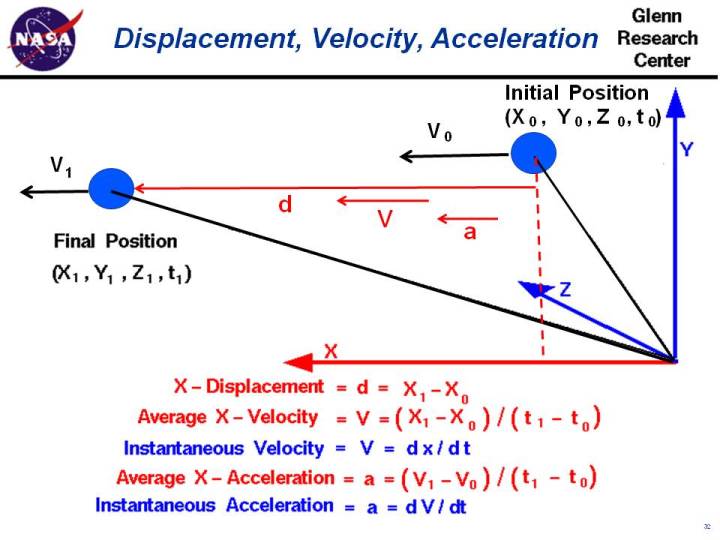
Initially, our object is at point "0", with coordinates x0, y0,
and z0 at time t0.
In general, the object moves through the domain until
at some later time t1 the object is at point "1" with coordinates
x1, y1, and z1.
We can specify the displacement - d in each coordinate direction
by the difference in coordinate from point "0" to point "1".
The x-displacement
equals (x1 - x0), the y-displacement equals (y1 - y0), and the z-displacement
equals (z1 - z0).
On this web page, for simplicity, we are only going to consider the x coordinate.
The displacement is then given by:
d = x1 - x0
Displacement is a
vector quantity, which means that displacement
has a size and a direction associated with it. The direction is from point "0" to
point "1".
The individual x-, y-, and z-displacements are the
components
of the displacement vector in the coordinate directions. All of the
quantities derived from the displacement are also vector quantities.
The velocity -V of the object through the domain
is the change of the location with respect to time.
In the X - direction, the average velocity is the displacement divided
by the time interval:
V = (x1 - x0) / (t1 - t0)
This is just an average velocity and the object might
speed up and slow down between points "0" and "1". At any instant, the object
could have a velocity that is different than the average. If we shrink the
time difference down to a very small (differential) size, we can define the
instantaneous velocity to be the differential change in position divided by the
differential change in time;
V = dx / dt
where the symbol d / dt is the differential from calculus.
(For younger students, you have just had your first lesson in calculus! ..
it wasn't so bad, was it? If this doesn't make sense, don't worry and just keep
reading .. it will make sense in a few years.)
When we initially
specify the location of our object with x0, y0, z0, and
t0 coordinates,
we should also specify an initial instantaneous velocity V0. Likewise at
the final position x1, y1, z1, and t1,
the velocity changes to a velocity V1.
Again, for simplicity, we are considering only the x-component of the velocity.
In reality, the velocity changes in all three directions. Velocity
is a
vector quantity and has both a magnitude and a direction.
The direction is the same as the the displacement direction from which we defined
the velocity.
The acceleration (a) of the object through the domain is the
change of the velocity with respect to time.
In the X - direction, the average acceleration is the change in velocity
divided by the time interval:
a = (V1 - V0) / (t1 - t0)
As with the velocity, this is only an average
acceleration. At any instant, the object
could have an acceleration that is different than the average. If we shrink the
time difference down to a very small (differential) size, we can define the
instantaneous acceleration to be the differential change in velocity divided by
the
differential change in time:
a = dv / dt
From Newton's
second law
of motion, we know that forces on an object produce accelerations. If we can
determine the forces on an object, and how the forces change with time, we can use the
equations presented on this slide to determine the acceleration, velocity, displacement
and, therefore, location of the object as a function of time.
Aeronautical engineers use this information to predict the
motion
of an aircraft, or the
flight
of a rocket.
Activities:







Guided Tours
-
 Forces, Torques and Motion:
Forces, Torques and Motion:

-
 Basic Aircraft Motion:
Basic Aircraft Motion:

-
 Cruising Aircraft:
Cruising Aircraft:

Navigation ..



- Beginner's Guide Home Page
|
