Weight and Balance Forces Acting on an Airplane
SUBJECT: Physics
TOPIC: Torques and Moments
DESCRIPTION: A set of mathematics problems dealing with torques and moments.
CONTRIBUTED BY: Carol Hodanbosi
EDITED BY: Jonathan G. Fairman - August 1996
Principle: Balance of forces produces Equilibrium
Gravity always acts downward on every object on earth. Gravity
multiplied by the object's mass produces a force called weight.
Although the force of an object's weight acts downward on every
particle of the object, it is usually considered to act as a single
force through its balance point, or center of gravity. If the object
has its weight distributed equally throughout, its balance point is
located at its geometric center. If the object has unequal weight
distribution, its balance point or its center of gravity may not be
at its geometric center. It is possible for the center of gravity to
entirely outside the boundaries of the object, as does a
boomerang.
The force that opposes the force of weight for an aircraft is
lift. The lift force must be greater than the weight for an airplane
to fly
For aircraft, it is important that the location of the center of
gravity fall within the limits specified by the design of the
aircraft. If it falls outside these limits, it will have adverse
effects on how the airplane will fly.
A moment or a torque is caused by a force acting on a body some
distance from the center of gravity. Its formula is:
torque = force x moment arm
where the force is always acting perpendicular to the moment arm.
In the diagram below, item A is at a distance X from
the fulcrum or pivot point, while item B is at distance
Y from the fulcrum. If the system shown is balanced, then the
product of A and X must equal the product of B
and Y
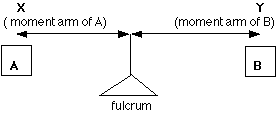
The product of the weight of item A and its distance from
the pivot point (X) produces a counterclockwise torque and the
product of the weight of item B and its moment arm Y
produces a clockwise torque. When the clockwise torques equal the
counter clockwise torques, the airplane or object is balanced along
that plane. in an airplane, any moment in front of the center of
gravity is considered a negative value, having a negative moment arm,
while and torque behind the center of gravity is considered to be a
positive value with a positive moment arm.
Finding the balance point: Given the following setup below, where
the length of the beam is 80 inches long but weightless. if we wish
to find the balance point of this system, or where to locate the
fulcrum, we first must set up an arbitrary zero reference point. This
can be located anywhere on the line of the beam. For this example, we
will choose the zero reference point to be at A.
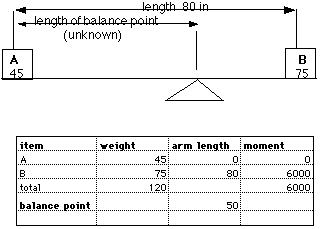
By constructing a simple chart of weight, moment arms and moments as
shown above, and placing the values in each space. Item A has
a weight of 45 pounds. Since the zero reference point was selected at
A, its arm length is 0. Zero times 45 is 0, so A's
torque or moment is zero. B weighs 75 pounds and its arm
length is 80 inches. Since 80 times 75 equals 6000 inches-pounds,
B has a torque of 6000 inches-pounds. The total weight is 120
pounds and the total moment 6000 inches-pounds, the balance point is
found by dividing the total moment by the total weight. This value is
50 inches located to the right of point A or since 80 - 50 =
30, it is also 30 inches to the left of B.
Checking these values, letting the moment arm of A be
negative, then
A's torque = force x distance = 45 pounds x -50 inches
= -2250 inches-pounds
B's torque = force x distance = 75 pounds x 30 inches =
2250 inches -pounds
Since the counterclockwise torque (-2250) and the clockwise torque
(2250) sum to zero, the beam will balance at the point located 50
inches to the right of point A.
Problem:
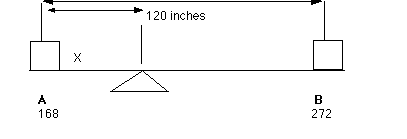
- Given the following figure below, where A has a weight
of 168 pounds and B has a weight of 272 pounds, and the
weightless beam is 120 inches long. Locate the center of gravity
where the fulcrum should be placed.
(Answer)
- Given the length of the weightless beam to be 120 inches, and
the weight at A to be 600 pounds with the center of gravity
to be located 4 feet to the right of A. Find the weight
necessary to produce equilibrium at B.
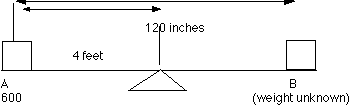
(Answer)
Extension:
An aircraft that has additional equipment installed on the plane or
replacements made by technicians needs to have the information about
its center of gravity updated.
Table for question 1
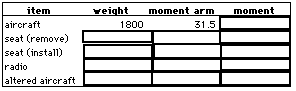
- An aircraft of known weight and center of gravity location is
going through alterations. A 30-pound seat located at 72 inches
with a 20-pound seat whose arm will be 73.5 inches. Also, a radio
of 30-pounds is to be installed at 30 inches. Find the new center
of gravity of the aircraft and complete the above table.
(Answer)
- An aircraft with an empty weight of 1,500 pounds and a center
of gravity (empty) of 28.4 inches was altered as follows:
- Two seats weighing 12 pounds each, located at 65.5
were removed.
(Answer)
- A structural modification increasing the weight by 28
pounds was made at 73 inches.
(Answer)
- A seat and safety belt weighing 30 pounds were installed at
70.5.
(Answer)
- radio equipment weighing 25 pounds was installed at 85
inches.
(Answer)
Find the following information: the new empty weight
is____________,
and the new location of the CG is__________.
(Answer)
Related Pages:
Aeronautics Activities
Aerospace Activities Page
Aerodynamics Index
Aircraft Weight
Aircraft Center of Gravity
Torques (Moments)
|
