
As a model rocket flies through the air, it rotates about a point called the center of gravity. The center of gravity is the average location of the weight of the rocket. The mass (and weight) is actually distributed throughout the rocket. And for some problems, it is important to know the distribution. But for rocket trajectory and maneuvering, we need to be concerned with only the total weight and the location of the center of gravity. How would you determine the location of the center of gravity?
Calculating cg
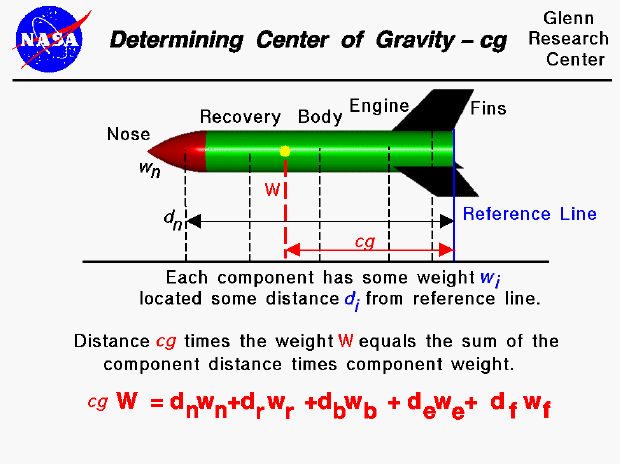
You can calculate the center of gravity. But in general, this is a complicated procedure requiring the use of calculus. This figure shows a simplified version of the center of gravity calculation that you can use. We assume that we already know the weight and location, relative to some reference location, of each of the major parts of the rocket: the nose, recovery system, body tube, fins, and engine. The total weight (W) of the rocket is simply the sum of all the individual weights of the components. Since the center of gravity (cg) is an average location of the weight, we can say that the weight of the whole rocket times the location of the center of gravity is equal to the sum of the weight of each component times the distance of that component from the reference location. (This is equivalent to saying the center of gravity is the mass-weighted average of the component locations.)
Components' Location
On the slide, we show the weight and distance of the nose relative to the reference line. The location of the reference line is arbitrary (it could be measured from the tip of the nose instead of from the base of the rocket as shown in the figure) but we have to remember where it is. The cg is a distance measured from the reference line as well. The "distance" of the nose (dn) is the distance of the center of gravity of the nose relative to the reference line. So we have to be able to calculate or determine the center of gravity of the nose and each of the other rocket components. For some simple shapes, finding the cg, or average location of the weight, is quite simple. For example, when viewed perpendicular to the axis, the body tube is rectangular. The center of gravity is on the axis, halfway between the end planes. There is a technique for determining the center of gravity of any general shape, and the details of this technique is given on another page.
Determining cg Mechanically
For a model rocket, there is a simple mechanical way to determine the center of gravity for each component or for the entire rocket:
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov