
 |
|
Glenn
|
This page shows the mathematical derivation of the compressible mass flow rate equation beginning with the definition of the mass flow rate and using information from the isentropic flow slide and the equation of state slide. A text version of this slide is also available.
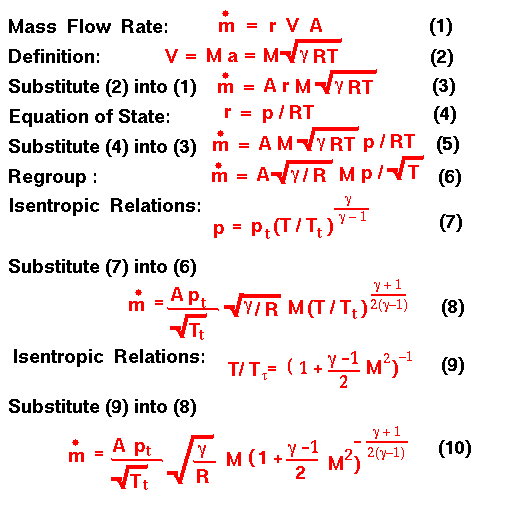
What does this equation tell us, and how can we use the equation?
If we had a flow through a tube at a fixed Mach number (fixed velocity), we could increase the mass flow rate through the tube by either increasing the area, increasing the total pressure, or decreasing the total temperature.
Similarly, if we had a tube with a known area, we could increase the mass flow rate by increasing the total pressure or decreasing the total temperature. The effect of Mach number is a little hard to determine because the form of the Mach number term is fairly complex. We can, however, use calculus to give us insight into the Mach number dependence. There is a technique in calculus to find the maximum (or minimum) value of a function by taking the derivative of the function and setting the resulting equation to zero. Let's apply this technique to the mass flow rate equation:

This result indicates that the maximum mass flow rate occurs when the Mach number is equal to one.
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov