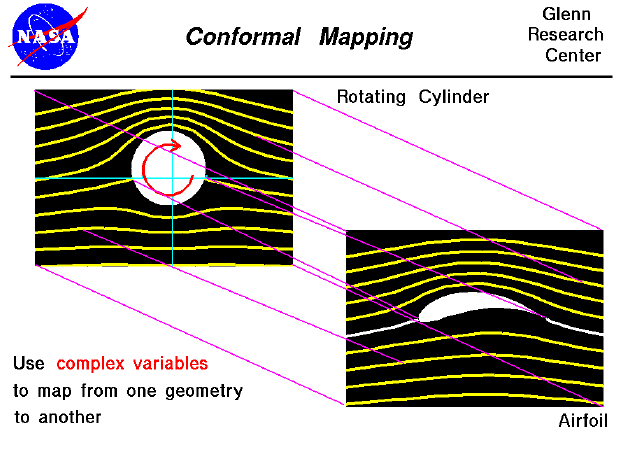

Conformal mapping is a mathematical technique used to convert (or map) one mathematical problem and solution into another. It involves the study of complex variables while in college. (Complex variables are combinations of real and imaginary numbers, which are taught in secondary schools). Under some very restrictive conditions, we can define a complex mapping function that will take every point in one complex plane and map it onto another complex plane. The mapping is represented by the purple lines in the figure.
Many years ago, the Russian mathematician Joukowski developed a mapping function that converts a circular cylinder into a family of airfoil shapes. The mapping function also converts the entire flow field around the cylinder into the flow field around the airfoil. Since we know the velocity and pressures in the plane containing the cylinder, we can derive the velocity and pressures around the airfoil using the mapping function. Knowing the pressure around the airfoil, we can then compute the lift. The computations are difficult to perform by hand, but can be solved quickly on a computer. Joukowski's transformations are computed in the FoilSim program.
You can see the effects of conformal mapping by using the FoilSim II Java Applet. If you want your own copy of FoilSim to play with, you can download it at no charge.
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov