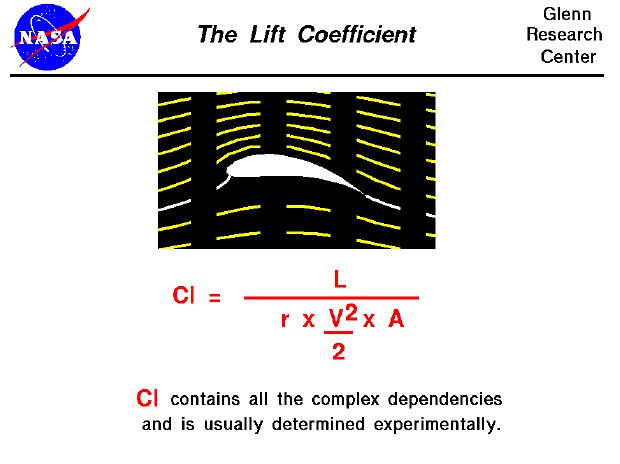

The lift coefficient is a number that aerodynamicists use to model all of the complex dependencies of shape, inclination, and some flow conditions on lift. This equation is simply a rearrangement of the lift equation where we solve for the lift coefficient in terms of the other variables. The lift coefficient Cl is equal to the lift L divided by the quantity: density r times half the velocity V squared times the wing area A.
Cl = L / (A * .5 * r * V^2)
Here is a way to determine a value for the lift coefficient. In a controlled environment (wind tunnel) we can set the velocity, density, and area and measure the lift produced. Through division, we arrive at a value for the lift coefficient. We can then predict the lift that will be produced under a different set of velocity, density (altitude), and area conditions using the lift equation.
The lift coefficient contains the complex dependencies of object shape on lift. For three dimensional wings, the downwash generated near the wing tips reduces the overall lift coefficient of the wing. The lift coefficient also contains the effects of air viscosity and compressibility. To correctly use the lift coefficient, we must be sure that the viscosity and compressibility effects are the same between our measured case and the predicted case. Otherwise, the prediction will be inaccurate.
For very low speeds (< 200 mph) the compressibility effects are negligible. At higher speeds, it becomes important to match Mach numbers between the two cases. Mach number is the ratio of the velocity to the speed of sound. So it is completely incorrect to measure a lift coefficient at some low speed (say 200 mph) and apply that lift coefficient at twice the speed of sound (approximately 1,400 mph, Mach = 2.0). The compressibility of the air will alter the important physics between these two cases.
Similarly, we must match air viscosity effects, which becomes very difficult. The important matching parameter for viscosity is the Reynolds number. The Reynolds number expresses the ratio of inertial forces to viscous forces. If the Reynolds number of the experiment and flight are close, then we properly model the effects of the viscous forces relative to the inertial forces. If they are very different, we do not correctly model the physics of the real problem and will predict an incorrect lift.
Navigation..
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov