|
|
Beginner's
Guide to Aerodynamics
Drag Equation - Level 2
Answers
In Drag Equation Level 1,
our pilot flew his first aircraft of the day. If you have not already done
so, you may want to go to this activity first to prepare you for the second
flight.
- Since the type
of aircraft has changed, so has it's wing area. Once again, in order
to work with our drag equation, we first need to find it's wing area.
NOTE: Find the areas of each common figure and obtain their
sum. You may assume the 2 right triangles are congruent.
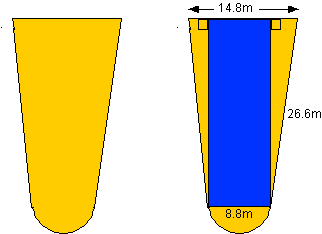
Work:
Using the Pythagorean theorem, length of the rectangle = 26.4 m
Total area = A(rectangle ) + 2 x A(triangle) + A(semicircle)
Total area = 8.8 x 26.4 + 2 x 1/2 x 3 x 26.4 + 1/2 x 3.14 x 4.42
= 341.92 m2 for one wing
683.84 m2 for both wings
- The drag coefficient
for our second aircraft was calculated at .365. When the pilot reached
the desired cruise speed of 400 mph, the air density was .00052 slugs/cu.
ft. What was the aircraft's thrust? NOTE: From the units
table in Drag Equation Level
1, you must first convert the area to the proper units. (1 inch
= 2.54 cm.)
Unit Conversion: 1 ft
= 30.48 cm = .3048 m. therefore, 3.28 ft = 1 m or 10.76 ft2 =
1m2
683.84 m2 x 10.76 ft2/m2 = 7358
ft2
Calculation: At
cruise, F = D = Cd x r x V2/2 x A = .365 x .00052 x (4002
\2) x 7358
111,700 pounds of thrust
- The thrust of the
first aircraft the pilot flew (Drag
Equation - Level 1) under these same conditions is 150,000 pounds.
If the 2 aircrafts weigh the same, which plane is more efficient?
The second aircraft since the Lift to Drag
ratio would be higher. (At cruise, Lift = Weight and Drag = Thrust)
|
