|
|
Beginner's Guide
to Propulsion
Forces in a Climb -Vectors
Answers
- Using the first
equation: L cos (c) + F sin (c) -D sin (c) - W = ma (vertical)
and the third equation: F -D = Fex , explain and show how
to obtain
the fourth equation: L cos (c) + Fex sin (c) - W = ma (vertical).
Factor sin (c) out of last two terms and
substitute Fex
for (F - D).
- Using the second
equation and the third equation, explain and show how to obtain the
fourth equation.
In the second equation, factor cos (c)
out of the first and third terms and substitute as in above.
- Why isn't
W multiplied by a sine or cosine?
Weight is a downward force, so it would
be W sin (90) or just W. (sin 90 is 1).
- Using the given
diagram, theorems/postulates of geometry, and vectors, explain each
term in the first two equations.
Vertical
Component.
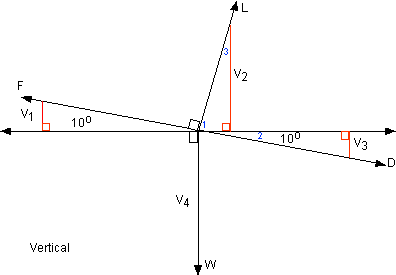
- V1
= F sin 10 positive (upward) vertical
V2
= L cos 10 positive vertical
- angle
1 + angle 2 = 90 Lift is perpendicular (vertical) to flight
path
angle
1 + angle 3 = 90 Acute angles of a right triangle are complementary.
Therefore
angle 1 + angle 2 = angle 1 + angle 3
Then
angle 2 = angle 3
Since
angle 2 = 10 then angle 3 must also.
V3
= D sin 10 negative (downward) vertical
V4
= W
Horizontal
Component
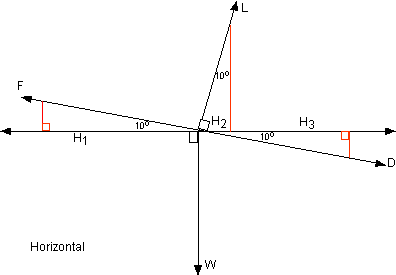
- H1
= F cos 10 Positive (forward)
H2
= L sin 10 Negative (backward)
H3
= D cos 10 Negative (backward)
"W"
only affects the vertical, not horizontal, or W cos 90 = 0
|
