|
|
Aircraft
Motion (Level 1)
Answers
- What is the smallest
angle in degrees between the lift and drag forces?
(a) 0o
(b) 90o (c)
180o (d) 270o (e) 360o
- What is the smallest
angle in degrees between the weight and lift forces?
(a) 0o
(b) 90o (c) 180o
(d) 270o (e) 360o
- What is the smallest
angle in degrees between the thrust and drag forces?
(a) 0o
(b) 90o (c) 180o
(d) 270o (e) 360o
- What is the smallest
angle in degrees between the weight and thrust forces?
(a) 0o
(b) 90o (c)
180o (d) 270o (e) 360o
- When an airplane
(or any object) is moving at a constant speed, the forces acting on
the airplane must be
(a) unbalanced,
which means that the total force is not zero.
(b) balanced,
which means that the total force is zero.
A fighter
jet is flying at 37,000 feet with a constant speed of 1,310 km/h.
The jet has a weight of 110,000 N and its engines provide a thrust
of 106,752 N (using afterburners).
- What is the jet's
height (altitude) in meters?
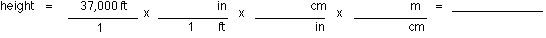
Step
1: Recall that 12 inches = 1 foot, 2.54 cm = 1 inch, and 100 cm
= 1 meter.
Step
2: Write these unit factors in their appropriate places in the
factor multiplication.
(a)
1.13 x 108 m (b) 61,248 m (c) 8,679 m (d) 356 m (e) 11,277.6
m
- What is the jet's
mass? [Hint: Use F = mag = W, where ag
= 9.8 m/s2.]
Step 1: force = weight = 110,000 N;
a = 9.8 m/s2 (acceleration due to gravity)
Step
2: mass = force / acceleration
(a)
520,120 kg (b) 11,224.49 kg
(c) 3,527 kg (d) 614,853 kg (e) 215 kg
- How much lift force
is being applied to the jet?
Realize that if the airplane's speed is
constant, the forces acting on the airplane must be balanced.
Force
of lift = Force of weight
(a) 512,128 N
(b) 5,634 N (c) 110,000 N
(d) 9,935 N (e) 106,752 N
- If the jet engines
are creating a thrust of 106,752 N, what is the drag force applied to
the jet?
Realize that if the airplane's speed is
constant, the forces acting on the airplane must be balanced.
Force
of drag = Force of thrust
(a)
512,128 N (b) 5,634 N (c) 110,000 N (d) 9,935 N (e) 106,752
N
Suppose the
jet engines are providing a thrust of 100,102 N while the drag force
is only 90,167 N.
- What is the total
unbalanced (or net) force on the jet?
Step 1: Fthrust = 100,102
N; Fdrag = 90,167 N
Step
2: Ftotal = Fthrust - Fdrag
(
Fnet = Ftotal)
(a)
512,128 N (b) 5,634 N (c) 110,000 N (d) 9,935
N (e) 106,752 N
- What will be the
jet's acceleration?
Step 1: F = 9,935 N; m = 11,224.49 kg
Step
2: acceleration = force / mass
(a)
0.89 m/s2 (b)
4.35 m/s2 (c) 0.36 m/s2 (d) 4,253 m/s2
(e) 65.3 m/s2
- If the jet is cruising
at 223.47 m/s and accelerates at 0.25 m/s2 for 1,530 seconds,
what is the jet's final speed?
Step
1: vi = initial velocity = 223.47 m/s; a = 0.25 m/s2;
t = 1,530 sec (vf = final velocity)
Step
2: a = ( vf - vi ) / t
a) 401.28
m/s (b) 605.97 m/s (c)
731.67 m/s (d) 634,521.6 m/s (e) 3,452 m/s
- Using the data
from the previous problem, calculate how far the jet traveled while
it accelerated during the 1,530 seconds.
Step 1: vi = 223.47 m/s;
a = 0.25 m/s2; t = 1,530 sec; di = initial distance
= 0 m (df = final distance)
Step
2: df = ( 1 / 2 ) at2 + vit +
di
(a)
401.28 m (b) 605.97 m (c) 731.67 m (d) 634,521.6
m (e) 3,452 m
- If the jet cruised
at a speed of 1,310 km/h for 2.53 hours, how far did it travel?
Step 1: v = 1310 km/hr.; t = 2.53 hr.
Step
2: d = vt
(a)
517.79 km (b) 4,639.00 km (c) 218.42 km (d) 6,547.23 km (e) 3,314.30
km
|
|
