|
|
Energy
Activity Answers
- A model glider
has a mass of 1 kg. How much potential energy does it have 2 meters
off the ground?
Ep = mgh = (1)(9.8)(2) = 19.6
j
- The same model
has a velocity of 2.2 m/s. How much kinetic energy does it have?
Ek = 1/2(m)V2 = (1/2)(1)(2.2)2 =
2.42 j
- If the same model
descends 2 meters and all it's potential energy is converted to kinetic
energy, what is the glider's change in velocity?
Ek = 1/2(m)U2
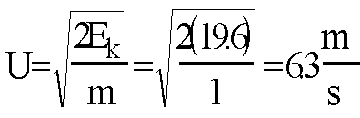
- A full-sized glider
has a weight of 4,900 N, while it's pilot has a weight of 825 N. If
it is 1,000 meters off the ground, how much potential energy do the
plane and pilot have?
Ep = mgh or Fwh = (4,900 + 825)(1,000) = 5,725,000
j
- The same glider
from Problem 4 has a velocity of 35 m/s. How much kinetic energy does
it have?
Ek = 1/2(m)V2 = 1/2 [(4.900 + 825)/9.8](352)
= 357,813 j
- The same glider
from Problem 4 has a velocity of 35 m/s. The glider descends 900 meters.
What is it's new velocity?
Ep = Fwh = (4,900 + 825)(900) = 3.63825
* 109 j
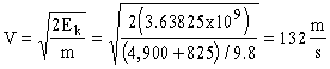
New Vel. = Old + Change = 35 + 132 = 167
m/s
- Compare the velocity
you calculated in Problem 6 to the speed of sound. Is this answer reasonable?
Why or why not?
167/346 = .48 Approximately 1/2 the speed
of sound. (Note: This speed is
faster than a B-17 Flying Fortress.)
|
