
At the end of 1901, the Wright brothers were frustrated by the flight
tests of their
1900 and
1901 gliders.
The aircraft were flown frequently up to 300 feet in a single glide. But neither
aircraft performed as well as predicted using the design methods
available to the brothers.
Based on their measurements,
the 1901 aircraft only developed 1/3 of the
lift
which was predicted by using the
Lilienthal data.
During the fall of 1901, the brothers began to question the aerodynamic
data on which they were basing their designs.
Their kite and glider
experiments convinced them that the accepted value of the
Smeaton
pressure coefficient (.005), which is used in both the lift and
drag
design equations, was in error. The brothers determined that
a value closer to .0033 would more accurately describe
their flight tests.
But this did not account for all of the performance differences. There was
still some questions about the lift and drag coefficients which
were obtained by Lilienthal and were being used by the Wrights.
The brothers decided to measure the lift and drag coefficients
themselves. They first built some small models of a wing and a
flat plate and attached them to a bicycle wheel.
Here is the configuration that the wheel would assume as it was
moved through the air.
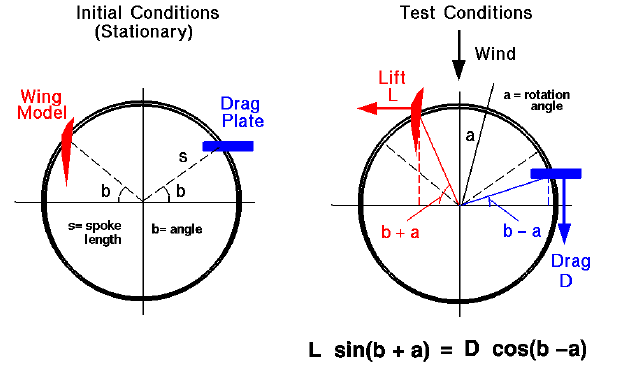
Initially the wing model and reference drag plate are located at
equal angles b about the centerline of the bike.
As the wind strikes the airfoil model it exerts a force to the left
as viewed from riders seat. The drag force on the plate is exerted
aft (down as viewed from above in the figure). The lift and drag forces generate
torques
about the hub of the wheel. The lift generates a counterclockwise torque
equal to the lift force L times the moment arm s times the
sine of the
sum of the initial angle b and the angle of rotation a
Tlift = L * s * sin(a + b)
The drag plate generates a clockwise torque equal to the drag force D
times the moment arm s times the
cosine of the
difference of the initial angle b and the angle of rotation a
Tdrag = D * s * cos(b - a)
When the wheel reaches an
equilibrium
condition, it no longer rotates and the angle a can be measured.
The equilibrium condition is that Tlift is equal to Tdrag
and then
L * sin(a + b) = D * cos(b - a)
Beginning with this relationship and using some information from high
school trigonometry, the brothers were able to relate the deflection
angle a to the ratio of the lift and drag. Here's the math:

They used the
Lilienthal data to predict the angle of rotation of the wheel
at which the drag of the
flat plate would exactly balance the lift of the wing.
They attached the wheel to the handles of a bicycle and rode through
the streets of Dayton to produce a wind over the models.
The test indicated a much lower value of lift from their model
than the lift predicted by the Lilienthal data. But the test conditions
were hard to control.
So the brothers decided to build a
wind tunnel
to produce a more controlled environment.
They would compare the
results
they found in the wind tunnel to
the performance they had measured during their kite and glider flights.
The wind tunnel tests were conducted from September to December of 1901. At
the conclusion of the tests, the brothers had the most
detailed data
in the world for the design of aircraft wings. They used this data to design the
1902 aircraft which overcame the problems encountered in 1900 and 1901.
They also used the data in the design of their propellers
for the 1903 aircraft.
Navigation..



- Beginner's Guide Home Page
|
