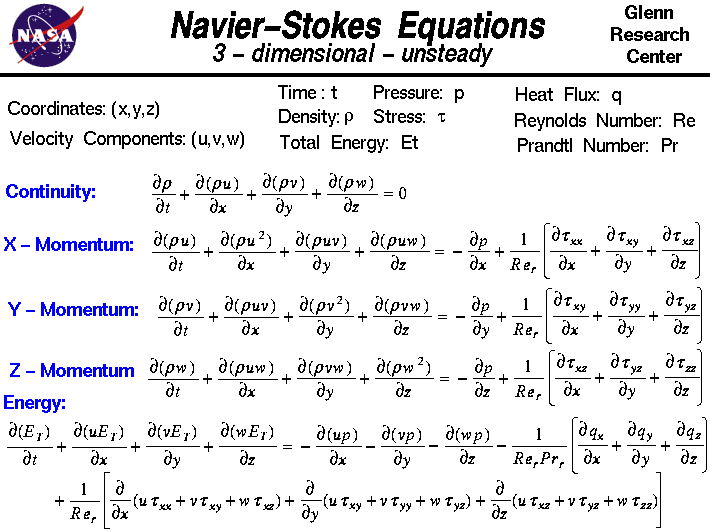
On this slide we show the three-dimensional unsteady
form of the Navier-Stokes Equations.
These equations describe how the velocity,
pressure,
temperature,
and
density
of a moving
fluid
are related.
The equations were derived independently by G.G. Stokes, in
England, and M. Navier, in France, in the early 1800's.
The equations are extensions of the
Euler Equations
and include the effects of
viscosity on the flow.
These equations are very complex, yet undergraduate engineering students
are taught how to derive them in a process very similar to the
derivation that we present on the
conservation of momentum
web page.
The equations are a set of coupled differential equations
and could, in theory, be solved for a given flow problem by using methods
from calculus.
But, in practice, these equations are too difficult to solve analytically.
In the past, engineers made further approximations and simplifications
to the equation set until they had a group of equations that they could solve.
Recently, high speed computers have been used to solve approximations
to the equations using a variety of techniques like finite difference, finite
volume, finite element, and spectral methods.
This area of study is called Computational Fluid Dynamics or CFD.
The Navier-Stokes equations consists of a time-dependent
continuity equation for
conservation of mass,
three time-dependent
conservation of momentum
equations and a time-dependent
conservation of energy equation.
There are four independent variables in the problem, the
x, y, and z spatial coordinates of some domain,
and the time t. There are six dependent
variables; the pressure p, density r,
and temperature T (which is contained in the energy equation
through the total energy Et) and three
components
of the velocity
vector; the u component is in the x
direction, the v component is in the y direction,
and the w component is in the z direction,
All of the dependent variables are
functions of all four independent variables.
The differential equations are therefore partial differential equations
and not the ordinary differential equations that you study in a
beginning calculus class.
You will notice that the differential symbol is different than the usual
"d /dt" or "d /dx" that you see for ordinary differential equations. The symbol
" " is
is used to indicate partial derivatives.
The symbol indicates that we are to hold all of the
independent variables fixed, except the variable next to symbol, when computing
a derivative. The set of equations are: " is
is used to indicate partial derivatives.
The symbol indicates that we are to hold all of the
independent variables fixed, except the variable next to symbol, when computing
a derivative. The set of equations are:
Continuity:  r/ r/ t + t +  (r * u)/ (r * u)/ x + x +  (r * v)/ (r * v)/ y + y +  (r * w)/ (r * w)/ z = 0 z = 0
X - Momentum:  (r * u)/ (r * u)/ t + t +  (r * u^2)/ (r * u^2)/ x + x +  (r * u * v)/ (r * u * v)/ y + y +  (r * u * w)/ (r * u * w)/ z = - z = -  p/ p/ x x
+ 1/Re * {  tauxx/ tauxx/ x + x +  tauxy/ tauxy/ y + y +  tauxz/ tauxz/ z} z}
Y - Momentum:  (r * v)/ (r * v)/ t + t +  (r * u * v)/ (r * u * v)/ x + x +  (r * v^2)/ (r * v^2)/ y + y +  (r * v * w)/ (r * v * w)/ z = - z = -  p/ p/ y y
+ 1/Re * {  tauxy/ tauxy/ x + x +  tauyy/ tauyy/ y + y +  tauyz/ tauyz/ z} z}
Z - Momentum:  (r * w)/ (r * w)/ t + t +  (r * u * w)/ (r * u * w)/ x + x +  (r * v * w)/ (r * v * w)/ y + y +  (r * w^2)/ (r * w^2)/ z = - z = -  p/ p/ z z
+ 1/Re * {  tauxz/ tauxz/ x + x +  tauyz/ tauyz/ y + y +  tauzz/ tauzz/ z} z}
Energy:  Et/ Et/ t + t +  (u
* Et)/ (u
* Et)/ x + x +  (v * Et)/ (v * Et)/ y + y +  (w * Et)/ (w * Et)/ z = - z = -  (r * u)/ (r * u)/ x - x -  (r * v)/ (r * v)/ y - y -  (r * w)/ (r * w)/ z z
- 1/(Re*Pr) * {  qx/ qx/ x + x +  qy/ qy/ y + y +  qz/ qz/ z} z}
+ 1/Re * { (u * tauxx + v * tauxy + w * tauxz)/ (u * tauxx + v * tauxy + w * tauxz)/ x + x +  (u * tauxy + v * tauyy + w * tauyz)/ (u * tauxy + v * tauyy + w * tauyz)/ y + y +  (u * tauxz + v * tauyz + w * tauzz)/ (u * tauxz + v * tauyz + w * tauzz)/ z} z}
where Re is the
Reynolds number
which is a similarity parameter that is the ratio of the scaling of the
inertia of the flow to the viscous forces in the flow. The q
variables are the heat flux components and Pr is the Prandtl number
which is a similarity parameter that is the ratio of the viscous
stresses to the thermal stresses.
The tau variables are components of the stress tensor.
A tensor is generated when you multiply two vectors in a certain
way. Our velocity vector has three components; the stress tensor has
nine components. Each component of the stress tensor is itself a
second derivative of the velocity components.
The terms on the left hand side of the momentum equations are called
the convection terms of the equations.
Convection
is a physical process
that occurs in a flow of gas in which some property is transported
by the ordered motion of the flow.
The terms on the right hand side of the momentum equations that
are multiplied by the inverse Reynolds number are called
the diffusion terms.
Diffusion
is a physical process
that occurs in a flow of gas in which some property is transported
by the random motion of the molecules of the gas.
Diffusion is related to the stress tensor and to the viscosity
of the gas. Turbulence, and the generation of
boundary layers,
are the result of diffusion in the flow.
The Euler equations contain only the convection terms
of the Navier-Stokes equations and can not, therefore, model
boundary layers. There is a special simplification of the Navier-Stokes
equations that describe boundary layer flows.
Notice that all of the dependent variables appear in each equation.
To solve a flow
problem, you have to solve all five equations simultaneously; that is
why we call this a coupled system of equations.
There are actually some other
equation that are required to solve this system. We only show five equations
for six unknowns. An
equation of state
relates the pressure, temperature, and density of the gas.
And we need to specify all of the terms of the stress tensor.
In CFD the stress tensor terms are often approximated by a turbulence
model.
Activities:
Guided Tours
Navigation ..


- Beginner's Guide Home Page
|
