Knots Versus Miles per Hour
SUBJECT: Aeronautics
TOPIC: Units
DESCRIPTION: A set of mathematics problems dealing with translating units for velocity.
CONTRIBUTED BY: Carol Hodanbosi
EDITED BY: Jonathan G. Fairman - August 1996
Knots is how the speed of aircraft and boats is measured.
Both miles per hour and knots is a speed which is the number of units
of distance that is covered for a certain amount of time.
1 knot = 1 nautical mile per hour = 6076 feet per hour
1 mph =1 mile per hour = 5280 feet per hour
For example, if a train is moving at 50 mph on a track, how would
you represent this speed in knots (even though trains are not usually
represented in knots)?
To do this problem easily, one must convert the speed in miles
per hour that the train is moving to the speed in feet per hour. This is accomplished
by multiplying by the number of feet in a mile.
That is,
(50 mph)*(5280 feet/ mile)=264,000 feet/hr
Now, convert the feet per hour to knots by multiplying by the knots conversion factor
(1 knot/ 6076 [feet/hr]).
(264,000 [feet/hr])*(1knot/6076 [feet/ hour]) = 43.4 knots
Exercises:
- Complete the following chart:
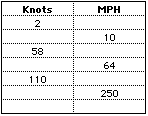
(answer)
In aerodynamics, speed is also measured by the Mach number, which is the
ratio of the speed of the object to the speed of
sound. Mach 1 means that you are traveling at the speed of sound or
661.7 knots, or
Mach 1 = 661.7 knots
How would you determine the speed of sound in mph?
Since
661.7 knots = (661.7 nautical miles/hr) (6076 feet/nautical
miles)
= 4,020,489.2 feet/hr
and
(4020489.2 ft/hr)/(5280 ft/mile)=761.5 mph
We can say that Mach 1 = 761.5 mph at sea level.
Since the speed of sound varies with the density of air ( or
whatever material it is transmitted through), one needs to determine
the density of the air the aircraft is flying through. To compute
this, we will use the chart shown below, called the International
Civil Aviation Organization Table, or I.C.A.O.
Notice as the altitude increased, the density of air decreases as
does the speed of sound in knots.
- Using the I.C.A.O. table below, complete the following chart:
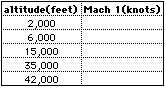
(answer)
- Now complete the following chart:
A
text only
version of this problem and answer are also available.
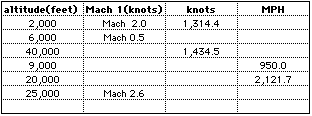
(answer)
I.C.A.O. Standard Atmosphere
Altitude
(Feet)
|
Density
|
Speed of Sound
(Knots)
|
|
0
|
.002377
|
661.7
|
|
1,000
|
.002308
|
659.5
|
|
2,000
|
.002241
|
657.2
|
|
3,000
|
.002175
|
654.9
|
|
4,000
|
.002111
|
652.6
|
|
5,000
|
.002048
|
650.3
|
|
6,000
|
.001987
|
647.9
|
|
7,000
|
.001927
|
645.6
|
|
8,000
|
.001868
|
643.3
|
|
9,000
|
.001811
|
640.9
|
|
10,000
|
.001755
|
638.6
|
|
15,000
|
.001496
|
626.7
|
|
20,000
|
.001266
|
614.6
|
|
25,000
|
.001065
|
602.2
|
|
30,000
|
.000889
|
589.5
|
|
35,000
|
.000737
|
576.6
|
|
36,089 *
|
.000706
|
573.8
|
|
40,000
|
.000585
|
573.8
|
|
45,000
|
.000460
|
573.8
|
|
50,000
|
.000362
|
573.8
|
|
55,000
|
.000285
|
573.8
|
* Geopotential of Tropopause
Related Pages:
Aeronautics Classroom Activities
Aerospace Activities Page
Aerodynamics Index
Mach Number
Interactive Atmosphere Calculator
|
