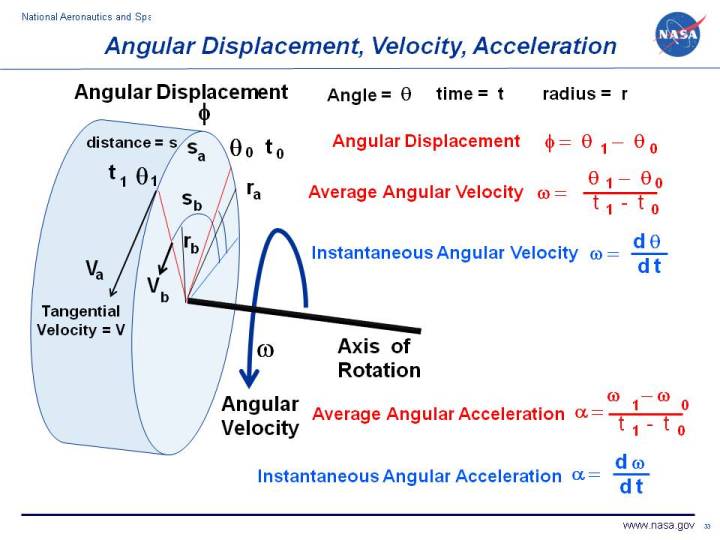
We live in a world that is defined by three spatial dimensions and one
time dimension. Objects move within this domain in two ways.
An object
translates,
or changes location, from one
point to another.
And an object
rotates,
or changes its orientation.
In general, the motion of an object
involves both translation in all three directions and rotation about
three principle axes.
On this page we will only consider the rotation of a solid object about
one axis.
The rotation of an object is similar to the translation in the number
of variables we must consider, but the notation is very confusing because
it has traditionally been described using Greek symbols. On the slide at the
top of the page we have used the traditional Greek notation.
To simplify Article 508 compliance, we will just spell out the names of the variables
here in the text, rather than use a symbol font.
Theta is the symbol that looks like a 0 with a horizontal line through it.
Phi is the symbol that looks like a 0 with a vertical line through it.
Omega is the symbol that looks like a curly w.
Alpha is the symbol that looks like a crossed ribbon.
Because the object rotates about an axis of rotation the simplest way
to describe the motion is to use
polar coordinates.
We can specify the angular orientation of an object at
any time t by specifying the angle theta the object has rotated
from some reference line.
Initially, our object is at orientation "0", specified by angle
theta 0 at time t0. We have drawn a red line on the disc
indicating the initial orientation.
The object rotates until
time t1 and the red line rotates to angle theta 1.
We can define an angular displacement - phi
as the difference in angle from condition "0" to condition "1".
phi = theta 1 - theta 0
Angular displacement is a
vector quantity, which means that angular displacement
has a size and a direction associated with it. The direction is important
for later mathematical processes, but the definition is a bit confusing. As the object
rotates from point "0" to point "1", it rotates about an axis, so the direction of the
angular displacement is measured along the axis. A positive value for the direction of the axis
is defined by the right hand rule. Extend your right hand as if to
shake hands with someone. Curve your fingers
with the base at point "0" and the tips going to point "1".
Your thumb points perpendicular to the plane of rotation
in the positive direction along the axis of rotation.
Angular displacement is measured in units of radians. Two pi radians equals
360 degrees. The angular displacement
is not a length (not measured in meters or feet), so an angular displacement is different
than a linear displacement. As the solid object rotates about the axis of rotation, all
of the points of the object experience the same angular displacement, but points farther
away from the axis move farther than points closer to the axis. On the slide we consider
two points; one is located at radius ra on the edge of the disk, and
the other is located at radius rb which is less than ra. As the object
rotates through the angular displacement phi, the point on the edge of the disk
moves distance sa along a circular path. The point at rb also moves in a
circular path, but the distance sb is shorter than the distance sa. In general,
the length of the circular path s is equal to
the radius r times the angular displacement phi, expressed in radians.
for angular displacement phi,
s = phi * r
ra > rb
sa > sb
The angular velocity - omega of the object
is the change of angle with respect to time.
The average angular velocity is the angular displacement divided
by the time interval:
omega = (theta 1 - theta 0) / (t1 - t0)
This is the average angular velocity during the time interval from t0 to t1,
but the object might speed up and slow down during the time interval.
At any instant, the object
could have an angular velocity that is different than the average. If we shrink the
time difference down to a very small (differential) size, we can define the
instantaneous angular velocity to be the differential change in angle divided by the
differential change in time;
omega = d theta / dt
where the symbol d / dt is the differential from calculus.
Angular velocity is a
vector quantity and has both a magnitude and a direction.
The direction is the same as the the angular displacement direction from which we defined
the angular velocity.
Angular velocity is measured in radians per second, or
revolutions per second, or revolutions per minute (rpm). Angular velocity is different
than linear velocity, which is measured in length per time (feet per second or meters per second).
All of the points of the object rotate at the same angular velocity, but points farther from
the axis of rotation move at a different tangential velocity than points
closer to the axis of rotation. The tangential velocity is measured along the circular path
s that we considered earlier. Tangential velocity V is equal to the angular
velocity omega times the radius r:
for angular displacement phi,
V = omega * r
ra > rb
Va > Vb
When we initially
specify the rotation of our object with theta 0, and
t0,
we should also specify an initial instantaneous angular velocity omega 0.
Likewise at the final position theta 1, and t1,
the angular velocity changes to an angular velocity omega 1.
The average angular acceleration - alpha of the object is the
change of the angular velocity with respect to time.
alpha = (omega 1 - omega 0) / (t1 - t0)
As with the angular velocity, this is only an average angular
acceleration. At any instant, the object
could have an angular acceleration that is different than the average. If we shrink the
time difference down to a very small (differential) size, we can define the
instantaneous angular acceleration to be the differential change in
angular velocity divided by the
differential change in time:
alpha = d omega / dt
In the same way that
forces
produce linear accelerations, a
torque
produces angular accelerations.
If we can
determine the torques on an object, and how the torques change with time, we can use the
equations presented on this slide to determine the angular acceleration,
angular velocity, and angular displacement
of the object as a function of time.
Aeronautical engineers use this information to predict the
rotations
of an aircraft in flight that become important for the stability and
control of an aircraft.
Activities:
Guided Tours
Navigation ..



- Beginner's Guide Home Page
|
