The lines CB and CA are vector quantities that
are supporting and acting opposite the object F . Draw a
line through point C parallel to the base support. Measure
the angle between CB and the line just drawn.
Since vectors CB and CA are not acting parallel
or perpendicular to the base of the stand, it is helpful to find
the components of each of these vectors. Components are vectors
that combine vectorally to form the resultant vector, in this case
CB or CA . For example, to find the components of
CA or CB one first needs to find the angle that
vector forms with the horizontal line, angle ACD or
angle BCE , see diagram below.
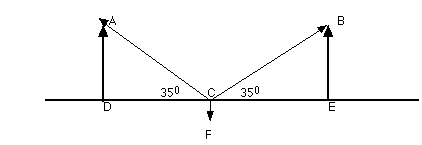
To find components of vector CB , form a right triangle
with CB as the hypotenuse. Since CB is a vector, or
a ray, one will be selecting a fixed portion of CB . Recall
the trigonometric functions of the sine (side opposite/
hypotenuse) and the cosine (side adjacent / hypotenuse). The sine
of angle BCE would equal side BE/CB , while the sine of
angle ACD = AD/ AC .
Let's assume that the angle ACD and angle BCE are
both 35° and that the weight represented by vector CF
is 100 newtons. Since the weight is static, and not moving, we can
assume all the forces are balanced. The vector represented by
CE (to the right) must be balanced by the vector CD
(to the left).The downward force of the weight represented by
CF must be balanced by the two upward forces DA and
EB . Since the two right triangles have two congruent
angles (35°) and two congruent sides, (FD and
CE ) the two triangle are congruent (Leg, Acute angle).
Because DA + EB = CF then DA = EB = 50
newtons.
By substitution, Sin angle BCE = BE/CB
Sin 35° = 50/CB
CB = 50 /Sin 35°
CB = 87.17 newtons
One can also find the measure of CE or CD using
the tangent function.
tan BCE = BE/EC
tan 35° = 50 /EC
EC = 50 /tan 35°
EC = 71. 4 newtons
Now use the following diagram to solve the problems below.
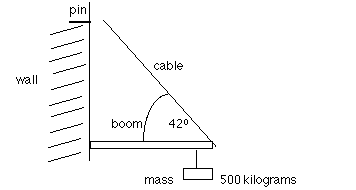
A load of 500 kg is suspended at the end of a horizontal boom
supported by a cable. The cable makes a 42° angle with the
boom and is attached to a wall by a supporting pin. You can assume
the boom's mass is negligible.
